Schon in der griechischen Mathematik (erste Aufzeichnungen 600 v.Chr.) finden wir die Lösung der Aufgabe, ein gegebenes Rechteck in ein flächengleiches mit einer gegebenen, neuen Seitenlänge zu verwandeln. Wenn ABCD das gegebene Rechteck und BG die neue Seitenlänge war, dann entstand mit dieser Konstruktion:
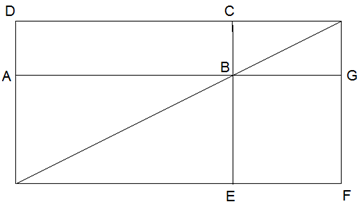
das Rechteck BEFG flächengleich zu ABCD. Diese Konstruktion hieß bei den Griechen ‚Flächenanlegen‘.
Spätestens nach der Entdeckung von Euklids Höhensatz oder Kathetensatz konnten die Griechen gegebene Rechtecke in flächengleiche Quadrate verwandeln.
Außerdem kannten die Griechen eine geometrische Darstellung der Gleichung, die wir heute
\( x∙y+ (\frac{x-y}{2} )^{2} = (\frac{x+y}{2})^{2} \)
schreiben und von den Griechen geometrisch dargestellt wurde:
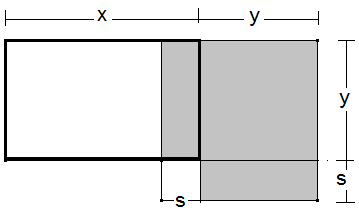
Hier wussten die Griechen: Die fett umrandete Fläche (x·y) ist ebenso groß, wie die grau unterlegte Fläche. Sie nannten dies ‚Flächenanlegung mit Fehlen‘. Was hier fehlt ist s² mit \( s = \frac{x-y}{2} \).
In der klassischen griechischen Mathematik wurden hauptsächlich geometrische Fragen gestellt und die Antwort durch geometrische Konstruktion gefunden. Mit den genannten Sätzen (Flächenanlegen, Höhensatz von Euklid und Flächenanlegung mit Fehlen) ausgerüstet konnten die Griechen folgende Aufgabe lösen:
Aufgabe:
Gegeben sind ein Rechteck ABCD mit der Fläche Q und eine Länge P.
Gesucht sind die Seitenlängen eines Rechtecks des Flächeninhalts Q dessen zwei verschiedene Seitenlängen zusammen die Länge P haben.
Dabei waren die Fläche Q und die Länge P durch Skizzen gegeben:

Heute formal gegeben durch x·y=Q und x+y=P.
Heute führt das auf die quadratische Gleichung x²-Px+Q=0.
Einzelschritte einer Handlungsvorschrift der Griechen zur geometrischen Lösung der Aufgabe:
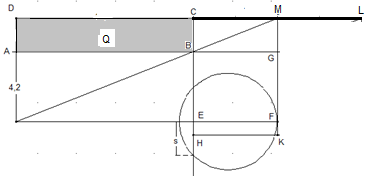
Konstruiere ein zum gegebenen Rechteck ABCD flächengleiches Rechteck EFGB mit der halben Länge P als Seitenlänge.
Konstruiere ein Quadrat HKGB in dessen Inneren die Rechtecke EFGB und HKFE liegen.
Trage |EH| an |EF| an, sodass E auf der Strecke H'F liegt.
Verwandle das Rechtecht HKFE in ein flächengleiches Quadrat. Konstruiere dazu den Kreis R mit dem Durchmesser |H'F|
Der Kreis R schneidet die Gerade BE in N. |EN|=s.
Das gesuchte Rechteck hat die Seitenlängen |BG|+s und |BG|-s.