Tiefpassfilter instabil. Für welche reellen Koeffizienten ai wird |(N+1)*( z^{N }| >>1?

Question

Aufgabe:

  Der Ausdruck ist nur symbolisch. Wennmman G(z) für N= 1, 2 oder 3 berechnet sieht man, dass der Nenner unter Form von (N+1)* z^{N} ist. Daraus folgt, dass das Realteil |(N+1)* z^{N }| ist und ich möchte die Werte erfahren für denen Modulo größer 1 ist.

Wie kann man erfahren für welche Werte von ai der Ausdruck |(N+1)*( z^{N }| >1 wenn \(a_i = \frac{1}{N+1} \)?

Answer 1

Aufgabe (a) ist eine normale geometrische Reihe, siehe https://de.wikipedia.org/wiki/Geometrische_Reihe

Wenn Du das berechnet hast, den Betrag und das Argument auf dem Einheitskreis berechnen.

Zu (b) Was ist das kriterium bei Euch für instabilität?

Comments

Hallo und vielen Dank!

Ja, Punkt a war einfach, das Problem ist bei Pkt. b. Ein Tiefpass ist instabil wenn das Realteil von z außerhalb des Einheitskreises liegt. darum habe ich G(z) für mehrere N's gerechnet und festgestellt, dass der Nenner unter Form von |(N+1)* z^N| ist. Also wenn N= 1/ai-1 größer als Null ist, dann wird das System instabil? also für ai <1?

---

Hi, die Übertragungsfunktion ergibt sich zu

$$ \frac{1}{N+1} \sum_{i=0}^N z^{-i} = \frac{1}{N+1} \frac{ \sum_{i=0}^{N} z^i }{ z^N }  $$

Damit hat die Übertragungsfunktion nur Polstellen im Ursprung und ist somit immer stabil.

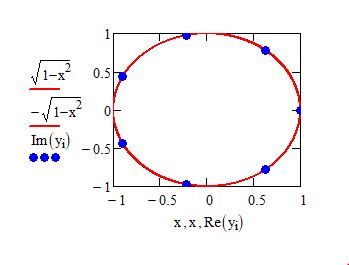
Die Übertragunsfunktion hat \( N \) Nullstellen, die auf dem Einheitskreis liegen und zwar von der Form \( e^{ i \frac{2 \pi}{n+1} k }  \) mit \( k = 1 ... n \)

Das sieht dann so aus:

Amplitudengang für \( n = 3 \)

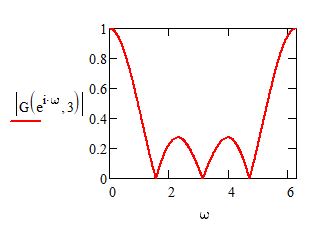
Phasenverlauf für \( n = 3 \)

Nullstellen für \( n = 6 \)