DGL-System Fundamentalsystem Wronski-Determinante und allgemeine Lösung

Question

Aufgabe:

Gegeben ist das Differentialgleichungssystem


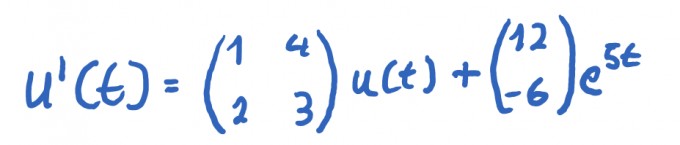
a) Bestimmen Sie ein Fundamentalsystem fur das zugehörige homogene System und berechnen Sie
die Wronski-Determinante.
b) Bestimmen Sie die allgemeine Lösung des inhomogenen Systems.

Problem/Ansatz:

Ich brauche bitte einen Plan wie ich an so eine Aufgabe herangehe, da ich das Thema nur so semi-verstanden habe. An sich DGL lösen geht einigermaßen, ich weiß an sich auch was ein Fundamentalsystem ist und wie man die wronski-Determinante berechnet, aber was ich dann mit einem DGL-System anfangen soll, weiß ich leider nicht.

Außerdem stört mich die Matrix, soll ich da die Determinante bestimmen oder was?

Schon Mal vielen Dank für jede Unterstzützung.

Answer 1

Hallo StormFusion,

es irritiert mich immer wieder, wenn Studenten überhaupt keinen Plan haben, wie man bestimmte Aufgabentypen löst. Werden Euch keine Beispiele gezeigt?

Anbei mein Beispiel. Schau es Dir an und versuche Deine Aufgabe analog zu lösen.

Comments

Bei diesem Thema trifft es sogar zu, dass wir nicht wirklich Beispiele dazu bekommen haben. War das letzte Thema dieses Semesters und gab dazu kein Übungsblatt, deswegen fällt es mir umso schwerer das Thema in den Kopf zu kriegen, vor Allem weil Differentialgleichungen nicht unbedingt ein Schema F haben.

Ich danke dir jedenfalls sehr für die Antwort, werde auf jeden Fall versuchen das durchzurechnen.

---

ich wollte mal fragen ob du mir bei dem b) - Teil der Aufgabe nochmal helfen könntest, die a) habe ich problemlos hinbekommen. Kannst dir ja mal meinen Kommentar zu der 2en Antwort dieser Frage anschauen.

PS. ich hoffe, im Forum ist duzen in Ordnung

Answer 2

Ein Anfang, hab mal ein bisschen gerechnet:

Comments

Dann hab ich die a) zumindest mal richtig, vielen Dank.
Die b) habe ich aber leider nicht hinbekommen, also die Variation der Konstanten, ich weiß eben nicht was ich da genau tun soll.

---

Hier mein Anfang mit dem ich aber nicht weiter gekommen bin und glaube ich auch nicht ganz richtig ist

---

Stell die Matrix Y auf und invertier diese. Y besteht aus den den Lösungen des homogenen Systems. Also

$$Y_{hom}=\begin{pmatrix} e^{5x} & -2e^{-x} \\ e^{5x} & e^{-x} \end{pmatrix}$$

 

---

Mein Versuch:

$$Y_{hom}^{-1}=\frac {1}{3}\begin{pmatrix} e^{-5x} & 2e^{-5x} \\ -e^{x} & e^{x} \end{pmatrix}$$

---

Dann kannst Du c' berechnen.