Berechne den Flächeninhalt des Quadrates!

Question

Aus einer kreisförmigen Blechscheibe mit d=20 cm soll ein möglichst großes Quadrat ausgeschnitten werden. Berechne den Flächeninhalt des Quadrates!

Answer 1

Hallo Anne,

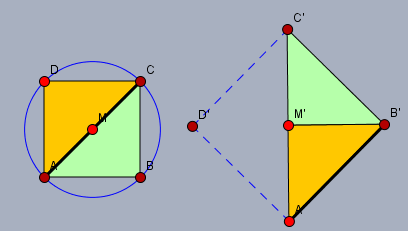
Links siehst Du das Quadrat \(ABCD\) in dem blauen Kreis. Seine Diagonale \(d=|AC|\) (schwarz) ist auch der Durchmesser des Kreises. Teile nun das Quadrat längst dieser Diagonalen in die beiden unterschiedlich gefärbten Dreiecke. Spiegele das grüne und ordne sie dann so an, wie im rechten Teil des Bildes zu sehen.

Es entsteht ein neues halbes Quadrat mit der Seitenlänge der Diaogonalen \(d\).

Also ist die Fläche \(A\) des linken Quadrats \(A = \frac 12 d^2\).

Answer 2

Der Durchmesser des Kreises entspricht dann denke ich der Diagonale des Quadrates.

A = 1/2 * d^2 = 200 cm²

Comments

Kannst du mir bitte erklären wie du auf das 1/2 kommst!

---

Du siehst in der nachstehenden Skizze, dass wenn man d^2 berechnet man anstatt des kleinen gewünschten Quadrates das doppelt so große Quadrat berechnet. Daher muss man wenn man die Diagonale statt der Seitenlänge quadriert das Ergebnis noch durch 2 teilen.

Answer 3

Siehe die Skizze von gorgar.

A = 4 * (10/√2)^2 = 200

Answer 4

a^2+a^2= d^2

2a^2 = 20^2 = 400

a^2 = 200

a= √200 = √(2*100) = 10*√2