Basis von R^4 bestimmen, die eine maximale Anzahl von Spalten einer Matrix enthält.

Question

Aufgabe:

\( A = \begin{pmatrix} 1 & 2  & 3 \\ 0 & 1 & 2 \\ -1 & 0 & 1 \\ -2 & -1 & 0 \end{pmatrix} \)

a)

Bestimmen Sie eine Basis von \( R^4 \) , die eine maximale Anzahl von Spalten von \( A \) enthält.
Begründen Sie Ihre Antwort.

b)

Geben Sie an, ob \( dim(A), rg(A), det(A), Kern(A) \) definiert oder nicht definiert sind und berechnen Sie es ggf.

Problem/Ansatz:

Wie soll ich am besten vorgehen? Wenn ich A gleich null setze und das LGS löse, habe ich eine unbekannte und somit unendlich viele Lösungen...

Comments

Von genauerer Fragestellung:

Titel: Bild einer Matrix berechnen und prüfen ob angegebene Vektoren im Bild sind.

Stichworte: matrix,vektoren,bild

Aufgabe:

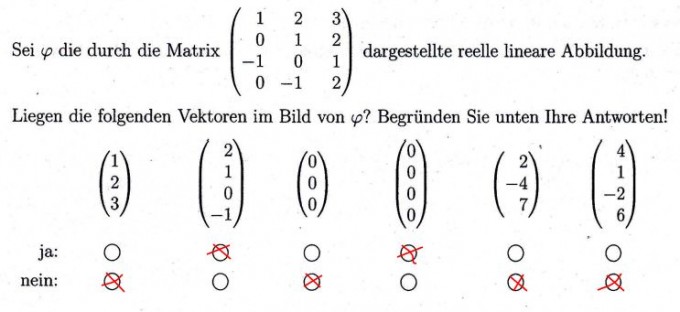
Problem/Ansatz:

Meine Lösung habe ich in das Bild eingefügt.

Um das Bild zu berechnen, habe ich die Matrix transponiert, in Zeilenstufenform gebracht und wieder transponiert und kam zu folgendem Ergebnis:

\( \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -1 & 2 & 0 \\ 0 & -1 & 4 \end{pmatrix} \)

Demnach wäre die Matrix \( \varphi \) auch zugleich mein Bild.

Ist das alles korrekt so?

---

Der letzte Vektor gehört auch zum Bild.

---

darf ich fragen wie du auf den kommst?

---

darf ich fragen wie du auf den kommst?

$$\begin{pmatrix}1& 2& 3\\ 0& 1& 2\\ -1& 0& 1\\ 0& -1& 2\end{pmatrix} \cdot \begin{pmatrix}15/4\\ -5/2\\ 7/4\end{pmatrix} = \begin{pmatrix}4\\ 1\\ -2\\ 6\end{pmatrix}$$

---

Wen meinst du mit "du"?

---

Damit meinte ich den User "mathef"

---

Gut, Dann hat doch Werner die Erklärung dazu geliefert.

Ist das jetzt ok.

Ich habe die Frage nun hierhin umgeleitet. Löschen schien mir unnötig. Abtippen wollte ich aber nicht.

---

Genau, die Frage war damit auch schon abgeschlossen. Gabs irgendwelche Probleme diesbezüglich?

---

Sie war immer noch "zum Löschen" gemeldet, weil ein Text in einem Bild zu sehen war. https://www.mathelounge.de/schreibregeln

---

Ah jetzt seh ichs, du hast also die Frage in eine andere (ähnliche) Frage von mir als Kommentar importiert.

Answer 1

Hallo

 1. Schritt: feststellen wieviele Spaltenvektoren lin. unabhängig sind, dann durch einen (oder 2) lin. unabhängige Vektoren zur Basis ergänzen.

Gruß lul