bräuchte mal Hilfe bei der Aufgabe e.) und wäre toll wenn jemand a.) bis d.) kontrollieren könnte.
Aufgabe:
Die kompexe Zahl z = a+ib setzt sich aus den beiden reellen Zahlen a,b (Realteil a, Imaginärteil b) und der imaginären Einhei i, mit der Eigenschaft i² = -1 zusammen. Diese werden beispielsweise zum Lösen von Polynomgleichungen des Typs x²+1 = 0 benötigt.
Stellen Sie das Ergebnis a.) bis d.) in der Form (Realteil + i Imaginärteil ) dar.
a.) Addieren Sie zu der Zahl z die komplexe Zahl y = c+id
b.) Subtrahieren Sie von der Zahl z die Zahl y.
c.) Multiplizieren Sie die Zahlen z und y
d.) Dividieren Sie die Zahl z durch y.
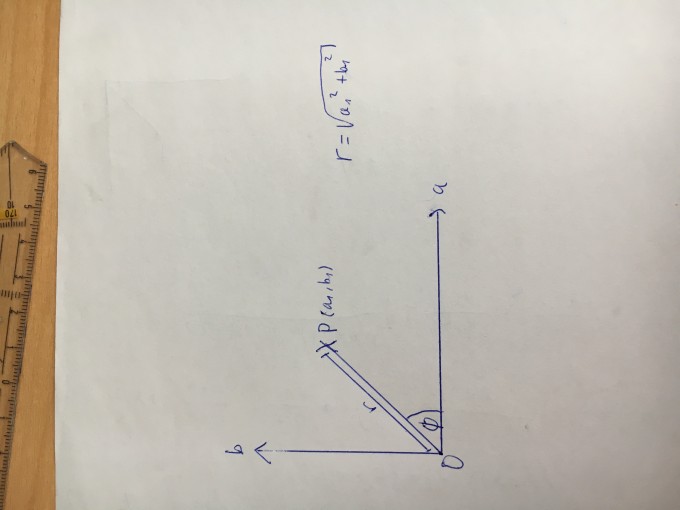
e.) Zeichnen Sie den Punkt P, gegeben durch die komplexe Zahl z mit den Koordinaten (a1 ,b1 )in eine rechtwinklige (komplexe) ab-Ebene ein. Verbinden Sie den Ursprung O mit dem Punkt P.
Die Entfernung von O nach P sei r und der Winkel zwischen OP und der positiven a- Achse sei Φ.
Drücken Sie a und b durch r und Φ sowie r durch a und b aus.
Geben Sie zusätzlich die Zahl z(r,Φ) als Funktion der Größen r und Φ ( in der sogenannte Polarform) an.
Problem/Ansatz: Ich lasse mal die Rechenschritte von a.) - d.) aus und schreibe die Lösungen hin.
a.) z + y = (a+c) + i(b+d)
b.) z-y = (a-c) + i(b-d)
c.) z*y = (ac-bd) + i(ad+bc)
d.) z/y = (ac+bd)/(c²+d²)+ i * (bc-ad)/(c²+d²)
e.) Fehlt mir noch was aber da verstehe Ich einfach nicht wie ich a und b durch r und Φ ausdrücke und auch nicht so richtig wie es in der Polarform ist.
PS : tut mir Leid ich weiß nicht wieso das Bild automatisch gedreht wird habe versucht es auf dem Laptop zu drehen und neu hochzuladen aber der dreht es immer zur Seite liegt bestimmt am Format.
Liebe Grüße MikroNewton