Integralrechnung: Infusion und Abbau von Medikamenten

Question

Für eine anstehende Klausur, wollte ich diese Textaufgabe zum Üben bearbeiten. Ich bin mir aber nicht sicher, ob ich sie richtig bearbeitet/gelöst habe.

Textaufgabe: Einer Patientin wird über eine Infusion ein Medikament ins Blut verabreicht. Anschließend wird das Medikament vom Körper annähernd gleichmäßig abgebaut. Der Graph beschreibt die Änderungsrate der Medikamentenmenge im Körper der Patientin.

a) Wie lange dauert die Infusion und wie viel ml des Medikaments wir der Patientin verabreicht?

b) Berechnen Sie, wie viel ml des Medikaments sich nach 5min, 10min, 15min, ... usw. im Blut der Patientin befinden.

c) Skizzieren Sie auch den Graphen, der die Medikamentenmenge in Abhängigkeit von der Zeit beschreibt. Welche Zusammenhänge lassen sich zwischen diesem Graphen und dem Graphen der Änderungsrate erkennen?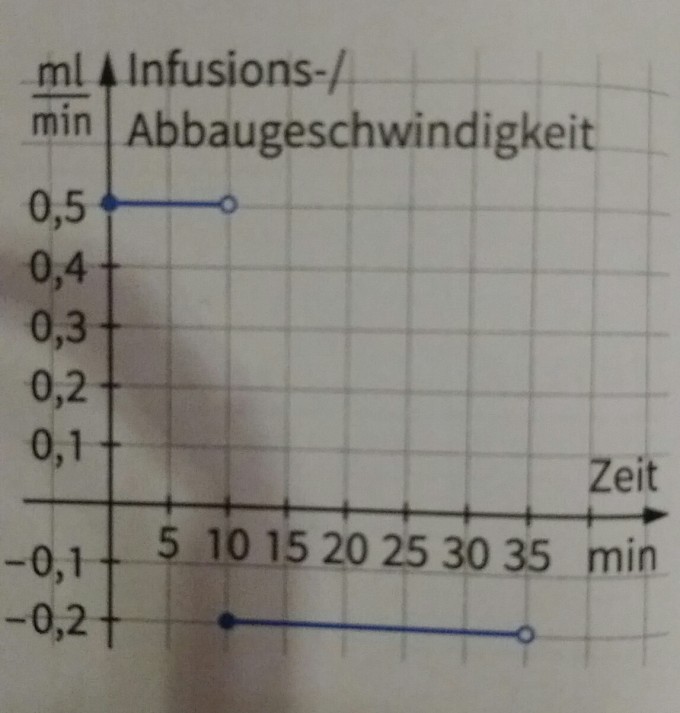

Hier meine Ansatz:

a) Dauer: 10min

    Medikament: 1ml

b) 5min-->0,5  10min-->1ml  15min-->0,8ml  20min-->0,6ml  25min-->0,4ml  30min-->0,2ml  35min-->0ml

c) Da habe ich den Graphen skizziert mit den Werten von b), sodass bei P(10/1) der Hochpunkt liegt.

Answer 1

Hallo

Infusion 10 Min mit 0,5ml/min wie kann man da auf 1ml kommen was ist 0,5ml/Min*10Min? Du hast anscheinend nicht verstanden was eine Änderungsrate ist, 0,5ml/min heisst dass die Menge in jeder Minute um 0,5ml zunimmt in 1/2 Minute z.B um 0,25 ml, in 3 Min um 1,5ml usw.

Menge im Blut: M(t)=0,5ml/Min*t (t in Minuten)

b) entsprechend am Anfang 5ml im Blut, dann 5ml-0,2ml/Min*t

c) die Graphen sollten eine von 0 an ansteigende Gerade sein, ab 10min dann eine abfallende Gerade, die bei t=35 bei 0 ist.

Comments

Also habe ich b) richtig gelöst?

---

Achso, habe jetzt den Fehler erkannt. Danke

---

Ich bin gerade dabei die gleiche Aufgabe zu rechnen, verstehe aber immer noch nicht, wie man auf die Werte bei b) kommt.

---

Hallo

ist dir klar wie man bei a) auf die Werte kommt? und damit bei b auf 5ml am Anfang,

dann wird es pro Minute um jeweils 0,2 weniger also  muss man jede Minute von dem was noch da ist 0,2ml abziehen also nach 1 Min 5-0,2=4,8 nach 5 Min:  5-0,2*5=4 usw

deshalb kann man rechnen 5ml -0,2ml/Min*t wenn man t in Minuten angibt.

wie man das noch genauer sagen kann weiss ich nicht,

Gruß lul

---

Ok danke das habe ich jetzt gemacht, sodass ich jetzt Werte raus habe. Allerdings verstehe ich immer noch nicht wie beispielsweise t=10 bei 1 ist oder t=35 bei 0 ist. Dort bekomme ich mit dieser Formel für t=10 -> 3 raus und für t=35 -> -2 raus.

---

Hallo

die t=35Min  sind seit Anfang der Infusion gerechnet.  nach den ersten 10 Min hört die auf. man hat 5mg intus, , dann werden 25Min lang um 0,2mg/min also um 25*0,2= 5mg  abgebaut Mund man ist auf 0 .

die t in der Formel für den Abba müssen immer zu den ersten 10 Minuten addiert werden, also 5-0,2*t für t =0 ist tges =t+10Min

ich hatte geschrieben: 5ml -0,2ml/Min*t wenn man t in Minuten angibt ich hätte dazu schreiben sollen Minuten nach dem Ende der Infusion, Wenn du die in c) verlangte Graphik richtig machst sieht du das .  du hast 2 Geradenstücke, die ersten 10 Minuten steigend mit o,5mg/min dann ab Punkt t=10Min , c=5ml , eine fallende Gerade mit der Steigung -0,2

Gruß lul

---

Also ich habe jetzt diese Werte raus:

5min=4

10min=4,8

15min=4

20min=3

25min=2

30min=1

35=0

Ist dies dann richtig?

---

Ich will mich nicht allzusehr einmischen
einmischen aber für mich ist das
die komischste Aufgabe seit langem.
Ein Graph auf dem nichts zu sehen ist,
eine Funktion ist nirgendwo angegeben
Der Graph ist die Änderungrate,
Aus welchem Nirwana kommen die
Werte ?

---

Nehme alles zurück.
Sachverhalt
In der ersten 10 min erhöht sich
die Medikamentenkonzentration
auf 10 min * 0.5 ml/min = 5 ml
Dann nimmt die Konzentration um
0.2 ml/min ab.

t : 10 min = 0
Konz ( t ) = 5 - 0.2 * t

Bei 25 min sind wir bei 0 angelangt.

---

Zu Julias Beitrag:

 5Min und 10 Min ist falsch

5Min 5*0,5=2,5

10Min 10*0,5=5

11Min 5-0,2*1=4,8

der Rest  ist dann richtig,

rechnet man die Zeit  nach der Infusion wieder von 0 an, also Zeit nach der Infusion, dann hat man 0 bei t=25Min.

lul