Umfang in Abhängigkeit x

Question

ich habe die Parabel p: y = -0,5(x-4)²+8. Zudem ist gegeben, dass Rechtecke A_nB_nC_nD_n wie folgt festgelegt werden: A_n,B_n ∈ x-Achse und C_n,D_n ∈ p. Dabei ist x die Abszisse der Punkte A_n.

Ziel der Aufgabe ist es zunächst die die Rechtecke für x1 = 1 und x2 = 2,5 zu zeichnen.

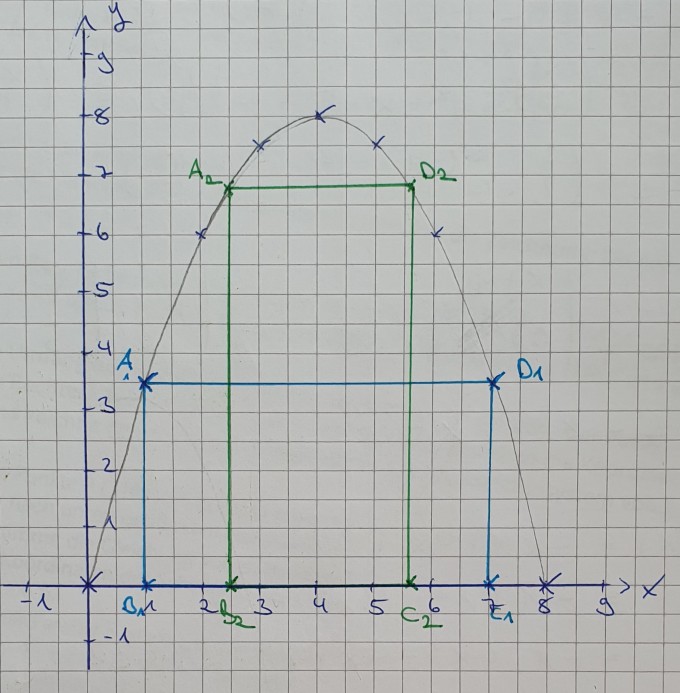
In der nächsten Teilaufgabe ist nun nach dem Umfang der Rechtecke in Abhängigkeit von x gefragt, hierbei brauche ich bitte Hilfe.

Vielen Dank :)

Answer 1

U = 2·g + 2·h = 2·(2·(4 - x)) + 2·(- 0.5·(x - 4)^2 + 8) = - x^2 + 4·x + 16

Skizze

~plot~ -x^2+4·x+16;[[0|4|0|30]] ~plot~

Comments

und wie ergibt sich die Grundfläche?:)

---

Grundfläche: g =  2·(4 - x)

Höhe: h = p(x)

---

U = g·h

Wer hat dir denn so'n Quatsch beigebracht ?

---

Ja aber wieso 2(4-x)?

---

U = g·h
Wer hat dir denn so'n Quatsch beigebracht ?

Niemand. Den Mist hab ich ganz allein verzapft. Aber nach deiner Anmerkung korrigiert.

Achtung Sasl: Beachte die korrigierte Antwort.

---

Ja aber wieso g = 2(4-x)?

Nimm das erste Rechteck mit x = 1

Dann ist 4-1 = 3 die halbe Grundseite des Rechtecks oder? Die muss ich mal 2 nehmen um die Komplette Grundseite zu haben.

---

tut mir leid ich stehe immer noch auf dem Schlauch :) weshalb nimmst du 4-1? welche 4?

---

x = 4 ist die Mitte der Grundseite, weil die Parabel achsensymmetrisch zur Geraden x = 4 ist, die durch den Scheitelpunkt geht.

---

Danke jetzt hab ich es! :)