Aufgabe:
ich hätte eine Frage, bei der Projektion eines Vektors auf einen anderen:
Text erkannt:
\( x \)
Problem/Ansatz:
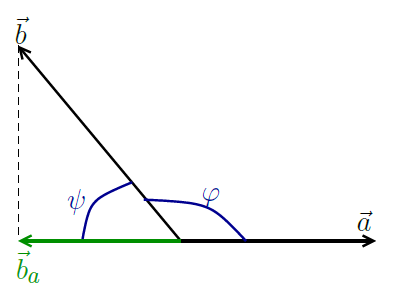
\( \cos (\varphi)=\cos \left(180^{\circ}-\psi\right)=-\cos (\psi)=-\frac{\left|\vec{b}_{a}\right|}{|\vec{b}|} \Leftrightarrow\left|\vec{b}_{a}\right|=-|\vec{b}| \cos (\varphi) \)
Ich verstehe nicht ganz, wieso cos(y) auf einmal -cos(v) ergibt. Ich verstehe, wieso wir -ba/b haben, da wir entgegengesetzte Orientierungen der Vektoren besitzen.
cos(v) * |b| entspricht ja |ba| -> |ba| = -|b| * cos(180° - v)
Verstehe die Überlegung von cos(y) = -cos(v) nicht. Wäre dankbar über eine Antwort.