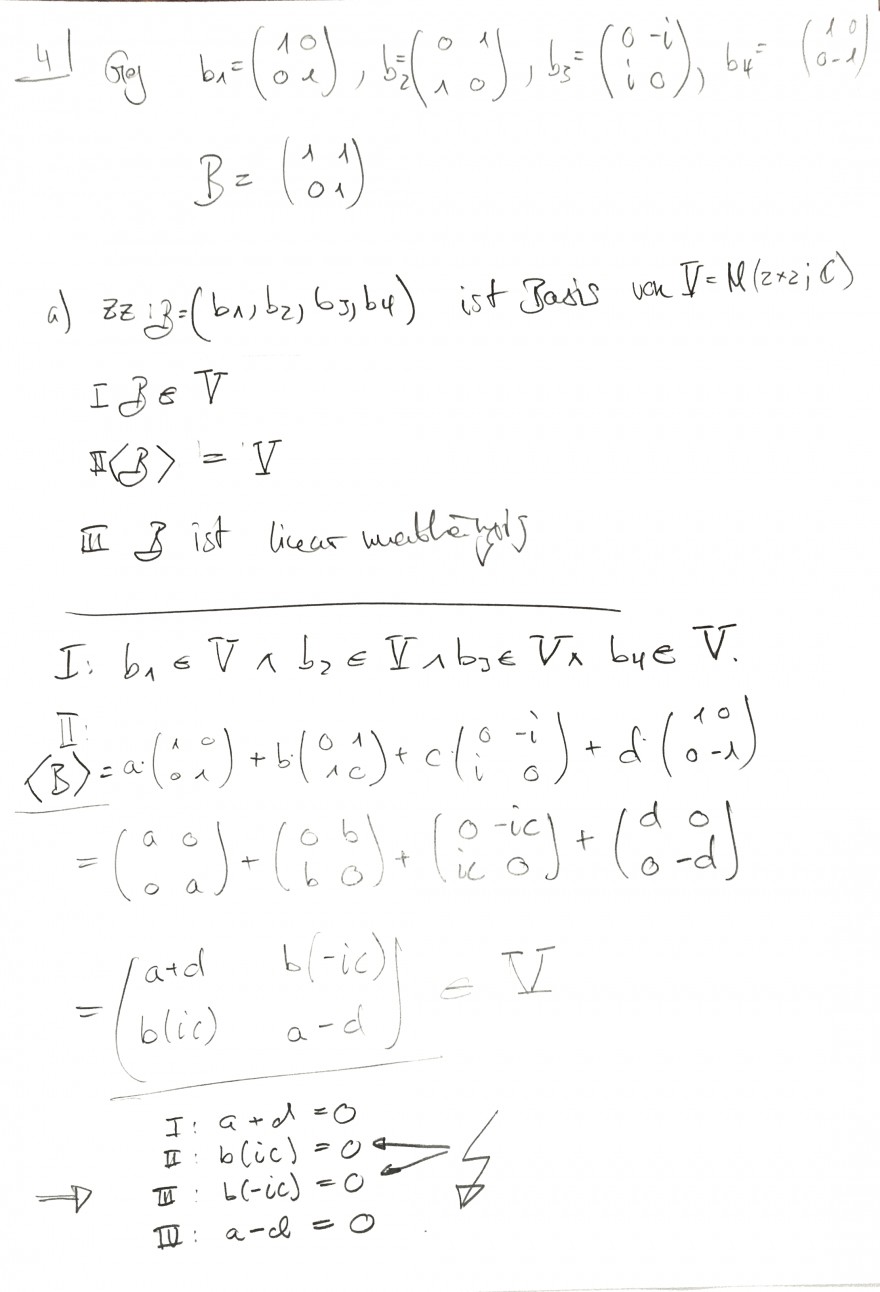Aufgabe:
Gegeben seien die komplexen Matrizen \(\sigma_{0}:=\left(\begin{array}{cc}{1} & {0} \\ {0} & {1}\end{array}\right), \sigma_{1}:=\left(\begin{array}{cc}{0} & {1} \\ {1} & {0}\end{array}\right), \sigma_{2}:=\left(\begin{array}{cc}{0} & {-i} \\ {i} & {0}\end{array}\right), \sigma_{3}:=\left(\begin{array}{cc}{1} & {0} \\ {0} & {-1}\end{array}\right), B:=\left(\begin{array}{cc}{1} & {1} \\ {0} & {1}\end{array}\right)\)
(a) Zeige, dass das Tupel \(\left(\sigma_{0}, \sigma_{1}, \sigma_{2}, \sigma_{3}\right)\) eine Basis des komplexen Vektorraumes Mat \(_{2 \times 2}(\mathbb{C})\) der \(2 \times 2\) -Matrizen bildet.
(b) \((2 \text { Punkte })\) Zeige, dass die Abbildung
$$ \begin{aligned} T: \operatorname{Mat}_{2 \times 2}(\mathbb{C}) & \rightarrow \operatorname{Mat}_{2 \times 2}(\mathbb{C}) \\ X & \mapsto X B-B X \end{aligned} $$
linear ist.
Bemerkung: Ich habe andere Bezeichnungen verwednet:
bei Aufgabe a) habe ich gemäss Bild die Basis \(\mathcal{B}\) genannt.
Die Basisimatrizen \(b_j\) mit j = 1,2,3,4 genannt.
Zur Lösung von a, habe Ich drei Schritte zu prüfen:
Zu prüfen 1.: \(\mathcal{B}\) ist in V.
Zu prüfen 2.: span(\(\mathcal{B}\)) = V.
Zu prüfen 3.: \(\mathcal{B}\) ist Linear unabhängig.
Lösung der drei Schritte:
Lösung zu 1.:
Habe ich sofort so gezeigt.
Lösung zu 2.:
Ich habe Koeffizienten \(a,b,c,d\) gewählt und die Menge aller Linearkombination gebildet.
\(a*b_1 + b*b_2 + c*b_3 + d*b_4 \begin{pmatrix} a+d & b(-i*c) \\ b(i*c) & a-d \end{pmatrix} \)
Frage 1: (ich glaube, ich habe hier bereits einen Fehler gemacht mit dem Basisvektor \(b_3\).)
Lösung zu 3.:
Beim zeigen der linearen Unabhängigkeit , greife ich das Resultat in "Lösung zu 2" auf und fahre mit der so erhaltenen Matrix fort und zeige, dass nur die triviale Nullsumme möglich ist.
Das führt auf folgendes Gleichungssystem
a + d = 0
b( i*c) = 0
b(-i*c) = 0
a - d = 0
Frage 2: Ich vermute dass die zweite und dritte Gleichung nicht richtig sind.
Bild: