Satz des Pythagoras Aufgabe

Question

Aufgabe:

Ein Brett mit unbekannten Maßen soll durch einen Gang transportiert werden. Der Gang ist 1m breit.

Frage:

Wie lang darf das Brett sein?

Wie hoch darf das Brett sein?

Problem/Ansatz:

Die Länge habe ich ausgerechnet, das wäre meine ich 2 mal Wurzel aus 2

Aber die Höhe  kann ich nicht berechnen.

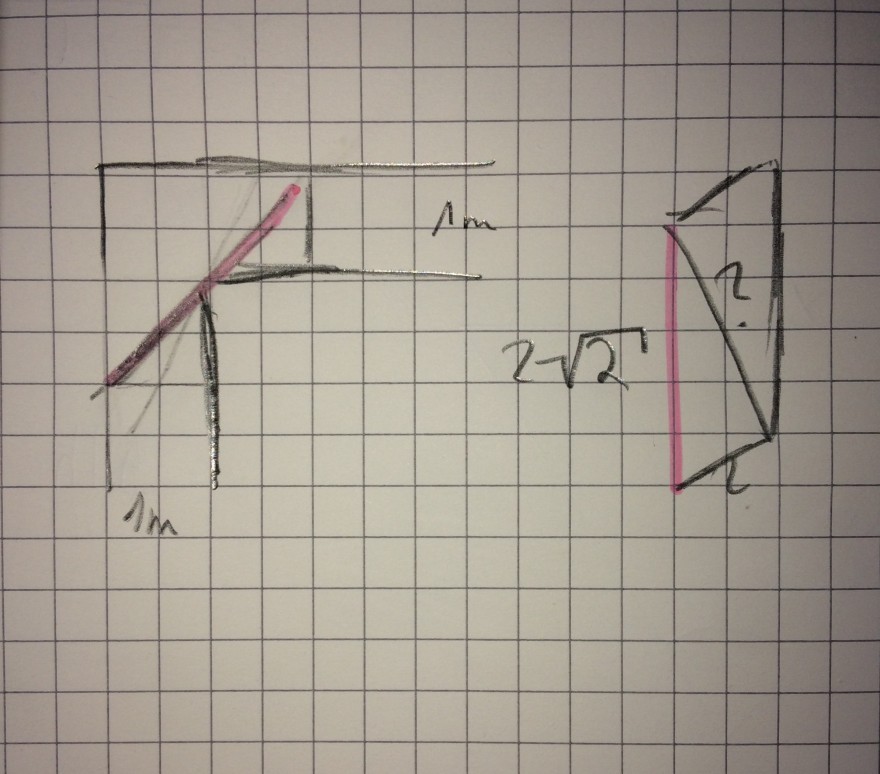
Text erkannt:

\( \begin{array}{|c|c|c|}\hline A & {1 \mathrm{m}} & {} \\ \hline & {} & {2-\sqrt{2}} & {} \\ \hline 1 & {} & {} & {} \\ \hline\end{array} \)

Answer 1

Hallo,

2*√2 ist richtig für die  maximale Länge, wenn das Bret so dünn ist wie Papier , für die Höhe und auch Tiefe des Brettes fehlen Angaben,

Annahme : Höhe = >  maximal Höhe des Flures

Comments

Wenn ich es richtig verstanden habe, meine Sie,

Für die Diagonale

1² 

^{plus 2 mal Wurzel aus 2}

^{= x hoch 2}

---

Hallo, es entstehen ja zwei Dreiecke um um die Ecke im Flur zu kommen , siehe deine Skizze d= √1²+1²   d= √2   und das nun zweimal  2√2

---

Verstehe ich nicht so ganz mit d meinen Sie die Diagonale?

---

Also was ist denn die Diagonale jetzt ? Und warum 12?