Hallo,
Aufgabe 2)
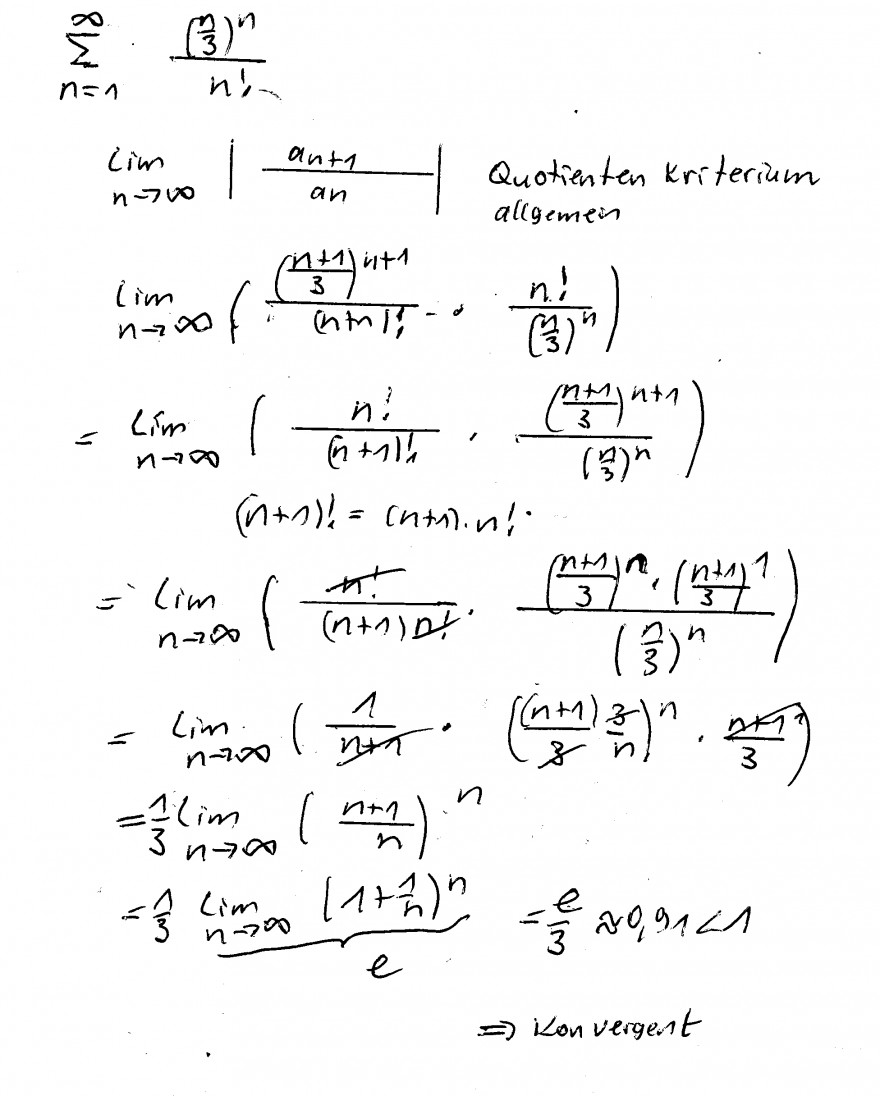
$$ $$ $$\sum \limits_{n=1}^{\infty} \frac{(n/3)^n}{n!}$$ $$ $$
Lösung durch Quotientenkriterium
allgemein: \( \lim\limits_{n\to\infty} \) | an+1/an|
an+1= (((n+1)/3)^(n+1))/(n+1)!
an= (((n/3)^(n))/n!
allgemein gilt:
(n+1)!= (n+1) *n!
eingesetzt:
=1/3 *e = e/3≈ 0.91 <1 ->konvergent
Aufgabe 1)
Lösung durch Quotientenkriterium
Lösungsweg ähnlich wie Aufgabe 2)
Lösung: 1/3 <1 ->konvergent