Laden eines Kondensators
An einem RC-Glied liegt eingangsseitig eine konstante Spannung U0. Der Verlauf der Kondensatorspannung beim Laden ist
\(u(t)=5V\cdot (1-e^{-\frac{2t}{s}})\quad (t ≥ 0s)\)
a) Berechnen Sie die mittlere Änderungsrate der Kondensatorspannung während der ersten Sekunde.
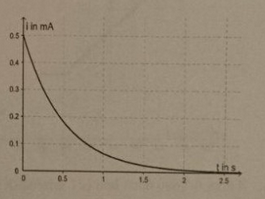
b) Die Graphik zeigt den zeitlichen Verlauf des Ladestromes i. Die t-Achse ist Asymptote des Graphen.
- Erklären Sie die Bedeutung dieser Tatsache im Hinblick auf den Ladevorgang.
Aus der Elektrotechnik ist bekannt, dass der Ladestrom proportional zur Spannungsänderung und der zugehörige Proportionalitätsfaktor gleich der Kapazität des Kondensators ist.
- Ermitteln Sie nachweisbar mit Hilfe der Graphik die Kapazität in (μF) des Kondensators.
c) Die angegebene Funktionsgleichung für u ergibt sich - von der Anfangsbedingung abgesehen - aus der Differentialgleichung
\(RC\cdot \frac{du}{dt}+u=U_0\quad für\quad u = u(t)\)
Darin bezeichnet r = RC die Zeitkonstante. Die DGL ist mit der Methode Trennen der Variablen zu lösen.
- Trennen Sie die Variablen und berechnen Sie die (allgemeine) Lösung der Differentialgleichung.
- Erklären Sie an Hand Ihrer Rechnung die verwendete Integrationsmethode.