Ausgehend vom Quadrat wird das Rechteck konstruiert. Bestimme das Verhältnis BE : AE.

Question

Aufgabe:

Ausgehend vom Quadrat ABCD wird das Rechteck AFBE konstruiert.

Bestimme das Verhältnis BE : AE.

Answer 1

Sei r der Radius des gestrichelten Kreises, dann gilt

AE=AM=ME= r und es ist Winkel AEB=90° (Thales).

Im rechtwinkligen Dreieck ABE wegen Pythagoras

(2r)^2 = r^2 + BE^2

==>   3r^2 = BE^2

==>    3 = BE^2 :  r^2

==>  √3 = BE : r  =    BE:AE

Comments

im rechtwinkligen Dreieck ABE wegen Pythagoras
\((2r)^2 = r^2 + BE^2\)

dann müsste ja \(AE = r = \frac 12 AB\) sein. Das ist aber nicht der Fall!

Answer 2

Für das gesuchte Verhältnis  BE:AE= v gilt im Dreieck ABE offensichtlich

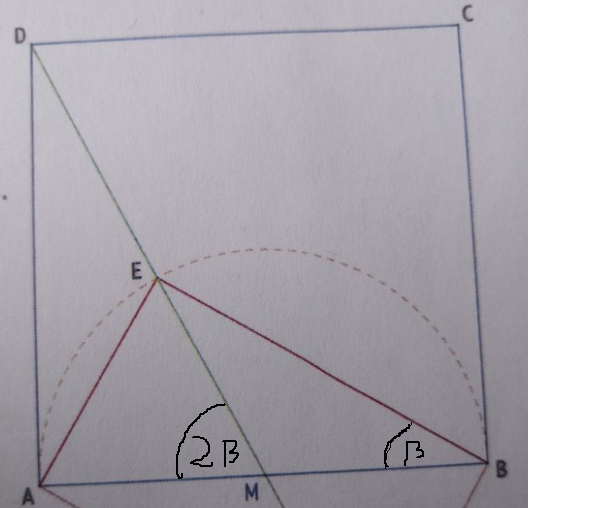
v = cot β.

Im Dreieck AMD gilt cot 2β = 0,5.

Nach Doppelwinkelformel für den Cotangens wird daraus

\( \frac{cot^2β-1}{2cot β} =0,5\) , also  \( \frac{v^2-1}{2v} =0,5\)

Das sollte schnittig und vergoldet aufzulösen sein.

Comments

Die Ähnlichkeit von  ΔAME und ΔFDE  liefert DE = DF ,
die Ähnlichkeit von  ΔABE und  ΔFAD  liefert  BE : AE  =  AD : FD .

Text erkannt:

\( x \)

Also wird  BE : AE  = AD : DE = 2 / (√5 - 1)  =  Φ .

---

Das ist ja nochmal ein ganzes Stück eleganter (weil wesentlich elementarer) als mein Vorgehen.

Respekt!

Leider ist kein Pluspunkt möglich, da es "nur" ein Kommentar ist.

Answer 3

Hallo Marko,

Eine schöne Aufgabe :-) !

Zeichne gleich große Winkel in die Skizze ein

Der Winkel \(\angle BAE\) (rot) sei \(\alpha\). Da \(\triangle AME\) ein gleichschenkliges Dreieck ist, ist auch \(\angle AEM = \alpha\) und somit auch der Scheitelwinkel \(\angle GED = \alpha\). Weiter ist \(\angle DGA = \alpha\), da \(\angle DGA\) ein Wechselwinkel zu \(\angle BAG\) ist. Daraus folgt, das \(\triangle EGD\) ein gleichschenkliges Dreieck und somit \(|GD|=|ED|\) ist.

Nun ist aber nach der klassischen konstruktion des goldenen Schnitts $$\frac{|AD|}{|ED|} = \Phi = \frac 12 \left( \sqrt 5 + 1\right)$$wegen \(|DM| = \frac 12 \sqrt 5 \cdot |AD|\) und \(|ED| = |DM| - \frac 12 |AD|\)

Und wegen der Ähnlichkeit der Dreiecke gilt auch $$\frac{|BE|}{|AE|} = \frac{|AD|}{|GD|} = \frac{|AD|}{|ED|} = \Phi$$