Aufgabe:
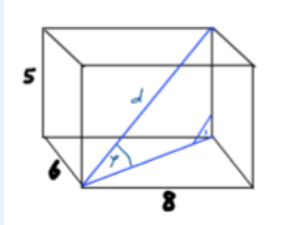
2) Raumdiagonale beim Quader 2
Aufgabenstellung:
Berechnen Sie die Größe des Winkels \( \phi \) zwischen der Raumdiagonalen d und der Grundfläche des Quaders!
\( \left( Lsg: 26,6^{\circ}\right)\)
Problem/Ansatz:
verstehe die Aufgabe bzw. komme nicht auf die Lösung.