Kegel Rechenaufgabe (Mantel und Volumen berechnen)

Question

Hallo, die Aufgabe lautet : Ein Kreisausschnitt mit dem Mittelpunktswinkel 90° und dem Radius 8 cm wird zu einem Kegel zusammengebogen. Berechne den Flächeninhalt des Mantels M und seinen Volumen V. Leider weiß ich nicht wie ich das berechnen soll, bzw. habe ich keine Ahnung wie man hier vorgehen muss.Könnte mir das bitte jemand Schritt für Schritt erklären? Das wäre wirklich lieb.

:)

Answer 1

Der Mantel ist ein Viertelkreis mit dem Radius 8 cm.

Die Grundfläche habe den Radius r, dann ist 2πr=8 und r=4/π.

Die Grundfläche ist dann G=π(4/π)²=16/π.

Die Höhe h des Kegels berechnet sich aus: (4/π)²+h²=64.

V=1/3·G·h.

Comments

warum ist es r=4/π?

---

Tut mir leid, meine Antwort war falsch. Es muss 4π heißen.

Answer 2

Hallo,

so sieht der Viertelkreis aus.

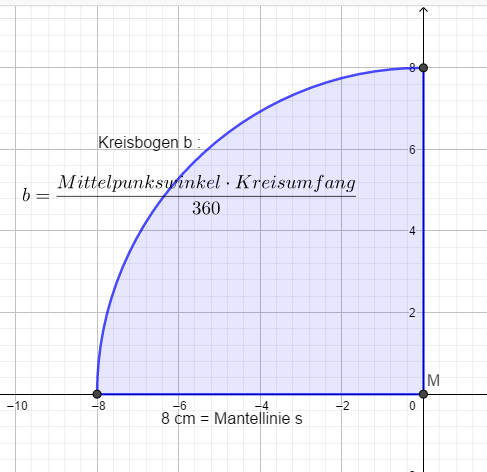
b ist der Umfang der Kegelgrundfläche = Kreis
s ist die Mantellinie des Kegels

Berechnung von b:
$$b =\frac{Mittelpunktswinkel\cdot Umfang }{360}$$

zuerst den Umfang berechnen:
$$U=d\cdot \pi\\ U=16\pi$$

$$b=\frac{90\cdot 16\pi}{360}=4\pi$$
Daraus folgt: Radius Kegelfläche = 2
 $$\text{Mantelfläche}\quad M=\pi\cdot r\cdot s=\pi\cdot 2 \cdot 8=16\pi\approx50,27cm^2$$
Volumen:
$$V=\frac{1}{3}\pi\cdot r^2\cdot h$$
h kann mit dem Pythagoras bestimmt werden:
$$h=\sqrt{s^2-r^2}=\sqrt{8^2-2^2}=2\sqrt{15}\approx7,75$$
$$V=\frac{1}{3}\pi\cdot 2^2\cdot 2\sqrt{15}=32,45cm^3\\$$

Comments

Sind b und der Umfang  nicht das selbe ?

Wenn nicht was ist der Unterschied ?

---

Ja, so ist es.

b ist der Umfang der Kegelgrundfläche = Kreis

---

Warum kommen dann jeweils zwei verschiedene Ergebnisse raus weil b=4pi und U=16pi

---

Da habe ich mich offenbar verschrieben oder verrechnet.

---

zuerst den Umfang berechnen:$$U=d\cdot \pi\\ U=16\pi$$

Das ist Unfug.

Richtig ist b = U = 4π