Hallo Lilli,
es ist schwierig zu verstehen, wie Deine Aufgabe genau lautet. Daran ändert Du auch nichts, wenn Du noch einmal die gleiche Aufgabe hier ein stellst.
Bei einer Aufgabe ist es wichtig zu wissen: was ist gegeben und was ist gesucht? Ich rate mal:
Es ist ein Würfel mit einer Kantenlänge von 14cm gegeben. Weiter ist ein Zylinder gegeben, der in den Würfel hinein passt, so dass seine Höhe und sein Durchmesser genauso groß sind, wie die Kantenlänge des Würfels von 14cm.
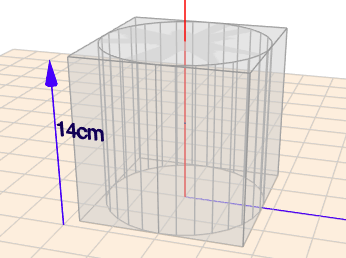
Das sieht so aus - oder?
Was ist gesucht?
... die aufgabe heißt man muss die Oberfläche berechnen ...
Die Oberfläche von was? Ok - hier sind nur Würfel und Zylinder und die Oberfläche des Würfels hast Du richtig mit \(1176 \text{cm}^2\) berechnet. Bleibt die Oberfläche \(O_z\) des Zylinders. Die setzt sich aus zwei Kreisen \(A_k\) mit dem Durchmesser 14cm und dem Mantel \(M\) des Zylinders zusammen. Rollst Du den Mantel ab, so hat er die gleiche Länge wie der Umfang des Grundkreises und seine Breite ist natürlich die Höhe des Zlinders. Also ist $$O_z = 2 \cdot A_k + M = 2 \cdot \underbrace {\left( \frac {14 \text{cm}}2\right)^2 \pi }_{\text{Kreisfläche}} + \underbrace{14 \text{cm} \cdot \pi}_{\text{Umfang}} \cdot 14 \text{cm} \\ \quad \approx 923,6 \text{cm}^2$$Gruß Werner
PS.: Versuche beim nächsten Mal die Aufgabe in kurzen Sätzen, mit einem Punkt am Ende, zu beschreiben. Und falls Du etwas nicht verstehst, so frage einfach nochmal nach. Bitte als Kommentar bei der gleichen Aufgabe.