ich habe ein Problem bei der Aufstellung von dem Funktionsterm

Question

Ein Polynom 3. Grades geht durch die Punkte P(0|-5) und Q(1|0) und berührt die x-Achse im Punkt R(5|0). Bestimme das Polynom! Wie mach ich das?

Answer 1

Hallo

 1. f(x)=ax³+bx²+cx+d

 1. die r Punkte  P,Q,R einsetzen gibt 3 Gleichungen, die vierte f'(x)=0 bei x=05 einsetzen

dann das einfache GS lösen-

Gruß lul

Answer 2

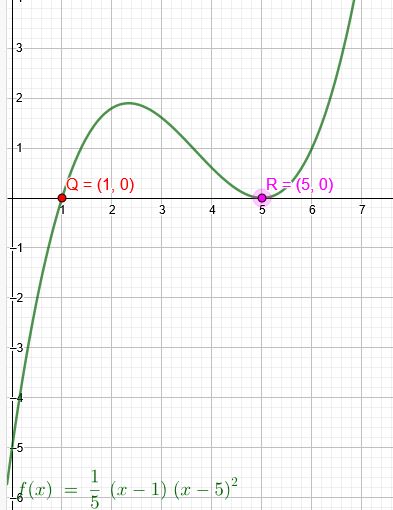
Ein Polynom 3. Grades geht durch die Punkte P$(0|-5)$ und Q$(1|0)$ und berührt die x-Achse im Punkt R$(5|0)$. Bestimme das Polynom!

Geht durch  Q$(1|0)$ einfache Nullstelle und berührt die x-Achse im Punkt R$(5|0)$ doppelte Nullstelle:

$f(x)=a(x-1)(x-5)^2$

P$(0|-5)$:

$f(0)=a(0-1)(0-5)^2=-25a=-5$

$a=\frac{1}{5}$

$f(x)=\frac{1}{5}(x-1)(x-5)^2$

Comments

Schöne Lösung!