Lineare Hülle und Basis bestimmen

Question

Aufgabe:

Mit den Vektoren
$$ \vec{v}_{1}=\left(\begin{array}{l} 3 \\ 8 \\ 7 \\ 3 \end{array}\right), \quad \vec{v}_{2}=\left(\begin{array}{c} 1 \\ 9 \\ 5 \\ -3 \end{array}\right), \quad \vec{v}_{3}=\left(\begin{array}{c} 2 \\ -1 \\ 2 \\ 6 \end{array}\right), \quad \vec{v}_{4}=\left(\begin{array}{c} -1 \\ 10 \\ 3 \\ -9 \end{array}\right) $$

bilden wir den Unterraum \( \boldsymbol{U}=\operatorname{Lin}\left(\vec{v}_{1}, \vec{v}_2, \vec{v}_{3}, \vec{v}_{4}\right) \) im \( \mathbb{R}^{4}, \) Finden Sie eine Basis für \( \mathbf{U} \). Bestimmen Sie die Dimension von \( U \).

Hinweis: Sind \(\vec{v}_{1}, \vec{v}_2, \vec{v}_{3}, \vec{v}_{4}\) linear unabhängig, so ist {\(\vec{v}_{1}, \vec{v}_2, \vec{v}_{3}, \vec{v}_{4}\)} eine Basis von U (siehe die Definition einer Basis).

Sind \(\vec{v}_{1}, \vec{v}_2, \vec{v}_{3}, \vec{v}_{4}\) linear abhängig, so müssen Sie aus \(\vec{v}_{1}, \vec{v}_2, \vec{v}_{3}, \vec{v}_{4}\) lineare unabhängige Vektoren, die U erzeugen, bestimmen.

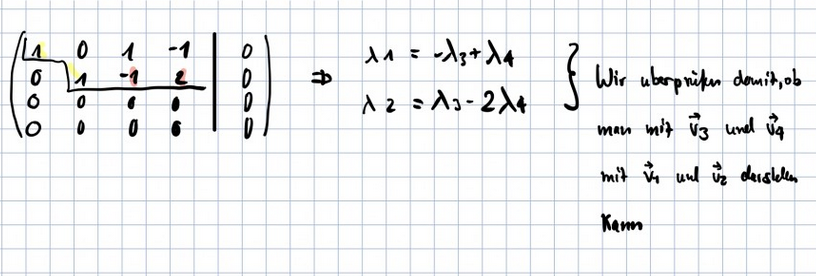
Ich habe soweit wie möglich berechnet und die Gaussche-Formel angewendet. Ich habe dann x1 und x2 bekommen mit den freien Variablen x3 und x4. Wie schreiben die jedoch in den Lösungen , dass d1 = -d3 +d4 entspricht. Man kann doch keinem Skalar einen weiteren Skalar zuweisen, oder verstehe ich da was falsch. x1 und x2. setzt man dann in die Linearkombination x1v1 + x2v2 + d3 + d4 ein.

Stimmt das?

Answer 1

Aloha :)

Schreibe die Vektoren als Spalten in eine Matrix. Die 4 Spaltenvektoren spannen den Unterraum \(U\) auf. Wenn du die Matrix nun durch elementare Spaltenumformungen auf Dreieckform bringst, fallen alle linearen Abhängigkeiten raus und übrig bleiben linear unabhängige Spaltenvektoren, also eine Basis von \(U\).

$$\left(\begin{array}{r} -S_3 &+S_4 & +2S_4 & +S_2\\ \hline 3 & 1 & 2 & -1\\8 & 9 & -1 & 10\\7 & 5 & 2 & 3\\3 & -3 & 6 & -9\end{array}\right)\to\left(\begin{array}{r} & & -S_2 & -S_2\\ \hline 1 & 0 & 0 & 0\\9 & 19 & 19 & 19\\5 & 8 & 8 & 8\\-3 & -12 & -12 & -12\end{array}\right)\to$$$$\left(\begin{array}{r} \vec b_1 & \vec b_2 &  & \\ \hline 1 & 0 & 0 & 0\\9 & 19 & 0 & 0\\5 & 8 & 0 & 0\\-3 & -12 & 0 & 0\end{array}\right)$$Es bleiben nur 2 linear unabhängige Basisvektoren übrig. Der Unterraum hat daher 2 Dimensionen.

Comments

Woher hast du -S3,+S4,+2S4 und +S2?

---

Das habe ich mir selbst ausgedacht. Dreieckform bedeutet, dass rechts oben ein Dreieck entsteht, das aus lauter Nullen besteht. Daher war die Idee, die erste Zeile auf die Form

\(1\;\;0\;\;0\;\;0\)

zu bringen. Dafür habe ich möglichst einfache Rechenoperationen gesucht. Dass dabei dann 3 gleiche Spalten entstehen war einfach nur Glück ;)

Answer 2

wenn du x1 und x2 durch die freien Variablen x3 und x4

darstellen kannst, heißt das auch, dass du  die Vektoren

e1 und e2 auch durch e3 und e4 darstellen kannst.

Eine Basis besteht also z.B. nur aus e3 und e4.

Du könntest es aber genauso gut anders herum machen und

e1 und e2 als Basis wählen.