Aufgabe:
Ein gleichschenkliges Dreieck mit einer 6cm langen Basis c hat eine Höhe hc bon 4cm. Diesem Dreieck soll, wie abgebildet ein Dreieck einbeschrieben werde. Berechnen Sie die Seitenlängen des einbeschriebenen Dreiecks so, dass sein Flächeninhalt maximal ist.
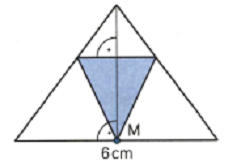
Problem/Ansatz:
Ich komme nur auf meine Hauptbedingung: (g*h)/2, aber nicht auf meine Nebenbedingung