eine Folge Komplexer Zahlen beweisen

Question

Aufgabe:

Sei (an) n ∈ N eine Folge komplexer Zahlen und a ∈ C. Beweisen Sie:

lim (n → ∞) an  =  a   ⇐⇒   (lim (n → ∞) Re(an) = Re(a)  und   lim (n → ∞) Im(an) = Im(a))

Comments

Hallo

 schreibe an=xn+iyn, a=x+iy und wende die Definition  von lim an.

Gruß lul

Answer 1

Hallo,

sei \(a_n:=x_n+iy_n\), die gegen \(a=x+iy\) konvergiert.

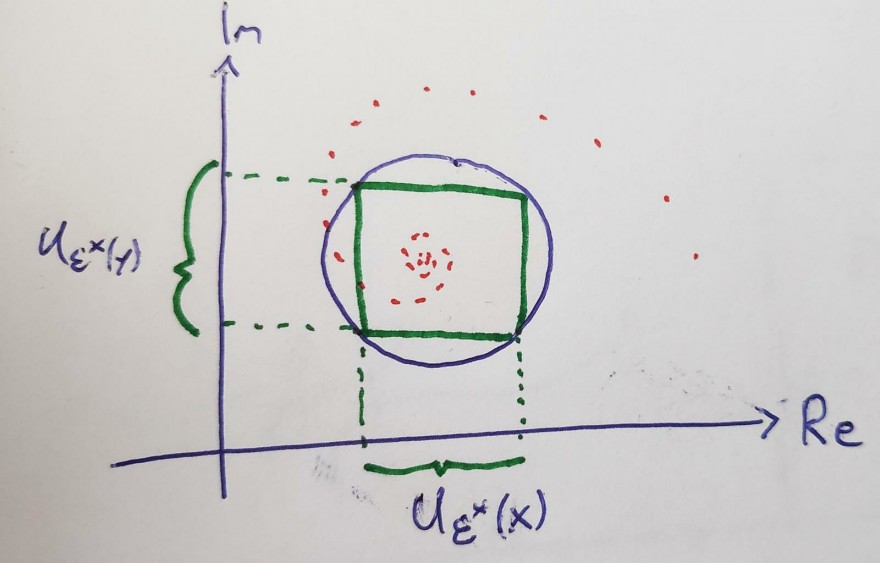
Nehmen wir an, dass ab einem bestimmten \(N\in \mathbb{N}\) alle Realteile in \(U_\varepsilon ^*(x)\) und alle Imaginärteile in  \(U_\varepsilon ^*(y)\) liegen. Wir können dann mit einer einfachen geometrischen Überlegung folgern, dass alle Folgenglieder in \(U_\varepsilon(a)\) (\(a\) sei der Grenzwert) liegen, setzt man \(\varepsilon :=\sqrt{2}\varepsilon ^*\).

Dann gilt nämlich:$$|a_n-a|=\sqrt{(x_n-a)^2+(y_n-y)^2}\leq \sqrt{2}\varepsilon ^*$$