Hallo,
mal angenommen, es soll geometrisch gezeigt werden, dass $$x + \frac 1x \ge 2$$dann erweitere ich das zunächst mal mit \(x\):$$x^2 + 1 \ge 2x$$und dazu folgendes Bild:
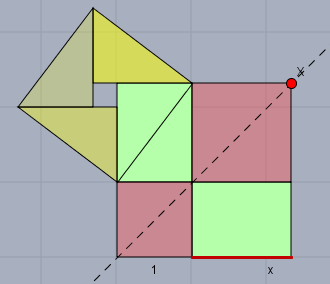
Das rote Quadrat links unten hat den Flächeninhalt \(1\) und rote rechts oben \(x^2\). Die Summe beider Quadrate ist größer als die Summe der grünen Rechtecke mit dem gemeinsamen Flächeninhalt von \(2x\). Das sieht man, wenn man die grünen Rechtecke diagonal zerschneidet und aus den vier rechtwinkligen Dreiecken (gelb) ein Quadrat mit der Seitenlänge der Diagonale formt. Dann verbleibt ein Loch in der Mitte. Nach Pythagoras wäre die Fläche dieses Quadrats gleich der Summe der beiden roten.
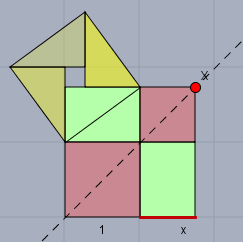
gilt natürlich auch, wenn \(x \lt 1\) ist. Nur bei \(x=1\) entsteht Gleichheit.
Wie kann man (4) aus (3) folgern?
indem man das arithmetische und geometrische Mittel aus \(x^2\) und \(1\) bildet: $$\frac 12 \left( x^2 + 1\right) \ge \sqrt{x^2 \cdot 1}$$
Gruß Werner