Aufgabe:
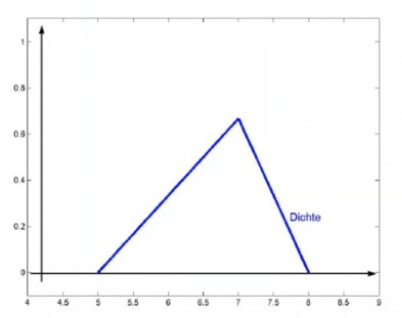
\( f(x)=\left\{\begin{array}{ll}0 & \text { für } x \leq 5 \\ \frac{1}{3} x-\frac{5}{3} & \text { für } 5 \leq x \leq 7 \\ -\frac{2}{3} x+\frac{16}{3} & \text { für } 7 \leq x \leq 8 \\ 0 & \text { für } x \geq 8\end{array}\right. \)
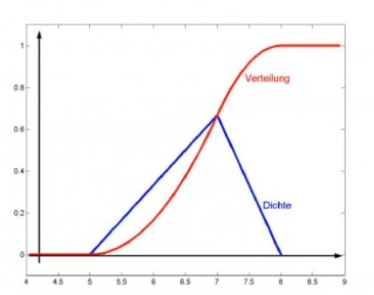
\( F(x)=\left\{\begin{array}{ll}0 & \text { für } x \leq 5 \\ \frac{1}{6} x^{2}-\frac{5}{3} x+\frac{25}{6} & \text { für } 5 \leq x \leq 7 \\ -\frac{1}{3} x^{2}+\frac{16}{3} x-\frac{61}{3} & \text { für } 7 \leq x \leq 8 \\ 1 & \text { für } x \geq 8\end{array}\right. \)
Problem/Ansatz:
Kann mir jemand erklären, was es qualitativ bedeutet, dass die Verteilung x größer gleich 8 = 1 sein soll ?
Schließlich kommt der Fall x größer gleich 8 ja offensichtlich nie vor, weshalb hat er dann eine Wahrscheinlichkeit von 100% ? Müsste es nicht heißen x kleiner gleich 8 = 100% ?
Die Rechnung selbst kann ich nachvollziehen.
Grüße