Wahrscheinlichkeiten einer Verteilungsfunktion ablesen/bestimmen

Question

Aufgabe:

Gegeben sei eine diskrete Zufallsgröße X, deren Verteilungsfunktion Fx durch den Graph im nachfolgenden Bild beschrieben ist.
Geben Sie Ihre Ergebnisse als Dezimalbrüche mit allen Nachkommastellen, zum Beispiel in der Form 0,123, an.

Problem/Ansatz:

Ich habe leider gar nicht mehr im Kopf, wie man so einen Verteilungsgraphen auswerten.

Bei P(X<=1) bin ich mir ziemlich sicher, dass es 0,25 ist. Aber bei X=2 und den anderen bin ich dann schon wieder unsicher. Rechnet man dann immer die Differenz aus?, also sprich: P(X=2) = 0,3-0,25 = 0,05?  Ich weiß es leider nicht mehr und habe auch keine Lösungen, die mir helfen würden.

Darum würde es mich freuen, wenn mir jemand helfen könnten. Vielen Dank :)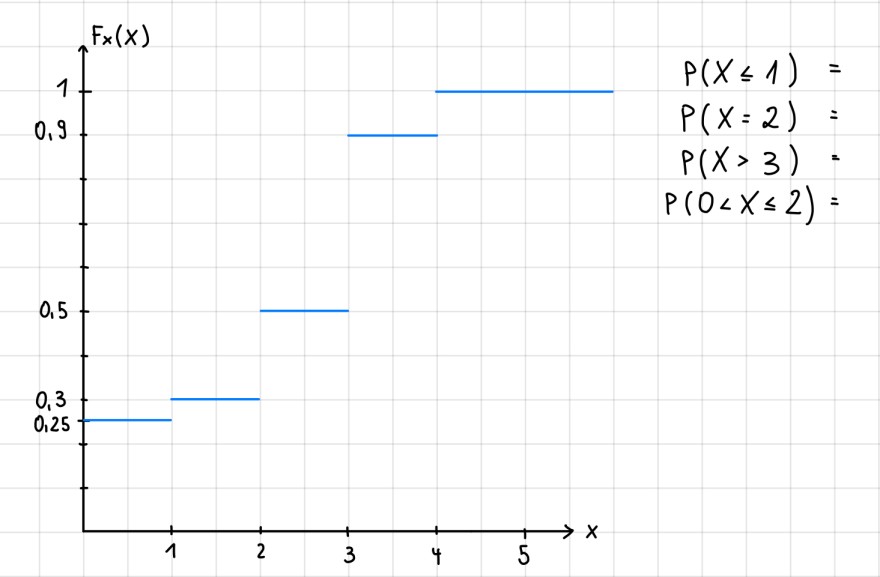

Text erkannt:

\( \begin{array}{l}p(x \leq 1)= \\ p(x=2)= \\ P(x>3)= \\ P(0<x \leq 2)=\end{array} \)

Comments

Bei P(X<=1) bin ich mir ziemlich sicher, dass es 0,25 ist.

Wie begründest Du das? Warum ist es nicht 0.3?

Answer 1

Die Verteilungsfunktion einer Zufallsgröße \(X\) ist definiert als \(F_X(k)=P(X\leq k)\). Damit gilt \(P(X\leq 1)=F_X(1)=0,3\). Die 1 gehört bereits zum zweiten Abschnitt, da eine Verteilungsfunktion rechtsseitig stetig ist.

Weiter ist \(P(X=2)=P(X\leq 2)-P(X<2)\). Das entspricht aber gerade der Sprunghöhe in der Verteilungsfunktion. Deine Rechnung stimmt da allerdings nicht, weil auch hier \(P(X\leq 2)=0,5\) ist und nicht 0,3.

Comments

Vielen Dank für die Erklärung :)