Hallo,
Die Funktion (keine mathematische!) atan2(), die von vielen Programmiersprachen zur Verfügung gestellt wird, dient dazu, einen Winkel eindeutig in einem Intervall von \((-\pi;\pi]\) zu berechnen. Dies ist mit dem üblichen Verdächtigen mathematischen Funktionen \(\arccos\) bzw. \(\arctan\) nicht möglich.
Gegeben sei ein Vektorenpaar \(a\) (rot) und \(b\) (blau). Der Winkel (blau) von \(Q\) bzw. \(a\) nach \(P\) bzw. \(b\) sei \(\varphi\)
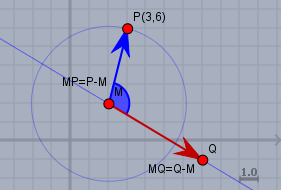
wobei hier:
$$a = \begin{pmatrix} a_x\\a_y \end{pmatrix}= \vec{MQ} = Q-M = \begin{pmatrix} q_x-m_x\\ q_y-m_y \end{pmatrix} \\ b = \begin{pmatrix} b_x\\b_y \end{pmatrix}= \vec{MP} = P - M = \begin{pmatrix} p_x-m_x\\ p_y-m_y \end{pmatrix} $$Nun ist $$\begin{aligned}a \times b &= \left|\begin{array}{cc} a_x& b_x\\ a_y& b_y \end{array} \right| \\ &= a_x \cdot b_y - a_y \cdot b_x = |a|\cdot |b| \cdot \sin \varphi \\ a \cdot b &= a_x \cdot b_x + a_y \cdot b_y = |a| \cdot |b| \cdot \cos \varphi\end{aligned}$$
Daraus folgt dann auch$$\tan \varphi = \frac{\sin \varphi}{ \cos \varphi} = \frac{|a|\cdot |b| \cdot \sin \varphi}{ |a| \cdot |b| \cdot \cos \varphi}= \frac{a \times b }{a \cdot b}$$
Bei dieser Division geht eine Richtungsinformation verloren, da der Arcustangens nur im Bereich von \([-\pi/2;\, \pi/2]\) eindeutig ist. Deshalb wird in vielen Programmiersprachen die besagte Funktion atan2() zur Verfügung gestellt, der beide Werte übergeben werden:
$$\begin{aligned} y &= a_x \cdot b_y - a_y \cdot b_x \\ x &= a_x \cdot b_x + a_y \cdot b_y \\ \varphi &= \text{Math.atan2}(y,x)\end{aligned}$$
(z.B. für Javascript) \(\varphi\) wird im Bogenmass zurück gegeben. Die Umwandlung in Grad geschieht durch Multiplikation von:
$$\begin{aligned} \text{rad\_to\_degree} &= 180./\text{Math.PI} \\ \varphi_{\text{deg}} &= \varphi \cdot \text{rad\_to\_degree}\end{aligned}$$
So liegt \(\varphi_{\text{deg}}\) im Intervall von \((-180°; \, +180°]\) und ist eindeutig.