Hallo Valentina,
man kann diese Aufgabe auch zeichnerisch mit Zirkel und Lineal lösen. Wie folgt:
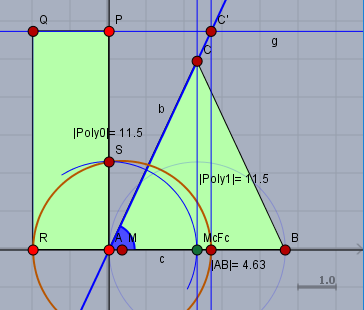
Zeichne eine Gerade \(c\) und trage einen Punkt \(A\) darauf ab. Übertrage den gegebenen Winkel \(\alpha = 65°\) (blau) in den Punkt \(A\). Der freie Schenkel sei \(b\) (blau). Übertrage die gegebene Fläche von \(11,5 \text{cm}^2\) als Rechteck \(APQR\) in der dargestellten Weise. Dabei spielt es keine Rolle welches Seitenverhältnis gewählt wird. Es muss lediglich \(|RA| \cdot |AP| = 11,5 \) sein! Ich habe hier \(2 \cdot 5,75\) gewählt.
Die Parallele zu \(c\) durch \(P\) sei \(g\). \(g\) schneidet \(b\) in \(C'\). Das Lot von \(C'\) auf \(c\) sei \(F_c\). Der Thaleskreis (braun) über der Strecke \(RF_c\) schneidet die Gerade durch \(AP\) oberhalb von \(A\) in \(S\). Der Kreis um \(A\) mit Radius \(AS\) schneidet \(c\) unterhalb des Schenkels \(b\) in \(M_c\) (grün). Der Kreis um \(M_c\) mit Radius \(M_cA\) schneidet \(c\) außer in \(A\) noch in \(B\).
Die Strecke \(AB\) ist die gesuchte Basis des gleichschenkligen Dreiecks mit \(|AB| \approx 4,63\).