Aufgabe: Möchte die Integration eines Graphen/Funktion zeichnerisch ausführen!
Problem/Ansatz:
Siehe Link, untere Problemstellung…: http://www.wichmann.dashosting.de/mathematische%20Basteleien/Integration.html
Graphische Integration
Es soll exemplarisch die Möglichkeit einer graphischen Integration für ein einfaches Beispiel aufgezeigt werden!
folgender Ansatz wird verwendet: f(f(x))=x*f'(f'(x))*k=r(x)*f'(f'(x)), siehe Bild 1! Dabei ist für mein Beispiel r(x)=k*x!
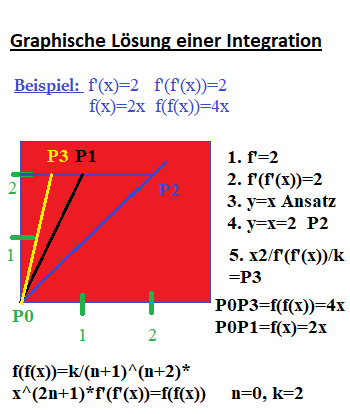
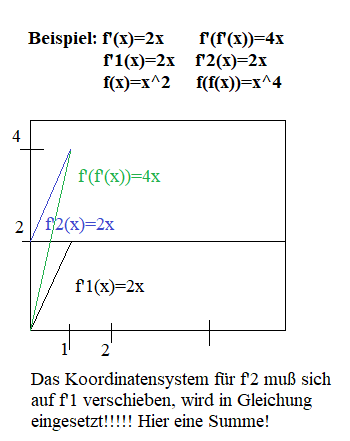
Die Bilder 1 und 2 stellen unterschiedliche Beispiele, der einfachen Anschauung und Konstruktion der Graphen wegen, dar!
Die Herleitung für dieses Beispiel:
f(x)=k/(n+1)*x(n+1)=k/(n+1)*x*xn, f'(x)=k*xn, f'(f'(x))=k*kn*xn*n
f(f(x))=k/(n+1)*(k/(n+1))n*xn*(n+1)*k/(n+1)*x(n+1), damit ergibt sich folgende Gleichung:
f(f(x))/f'(f'(x))=r(x)=k/(n+1)(n+2)*x(2n+1), für dieses gewählte Beispiel!
damit ist f(x)aus f(f(x)) ermittelbar, siehe Bild 2!
Dies ist ein einfaches Beispiel, wie schon gesagt, exemplarisch für eine graphische Integration! Die Funktion f(f(x)) möchte ich als Stützfunktion bezeichnen, da ein Wert den anderen bestimmt und daraus sich die Funktion f(x) ableiten lässt! Die Funktion r(x) muß dabei jeweils für einen anderen Funktionstypen für f(f(x)) modifiziert werden! ( zb. ex, 1/xn)!!!!
Damit lässt sich ein Integral graphisch/rechnerisch aus r(x) und f'(f'(x)) ermitteln!
Nachweis für r(x) für dieses Beispiel
f'(f'(x))*f''(x)=(f(f'(x)))' Kettenregel, f'(f'(x))*r(x)=f(f(x)) graphische Integration, daraus folgt:
f(f(x))=r(x)*(f(f'(x)))'/f''(x)
f(x)=k/(n+1)*x(n+1), f'(x)=k*xn, f'(f'(x))=k*knxnn, f''(x)=k*n*x(n-1)
r(x)=k/(n+1)(n+2)*x(2n+1), r(x)/f''(x)=x(n+2)/((n+1)(n+2)*n)
(f(f'(x)))'=k/(n+1)*k(n+1)*(n2+n)*x(n2+n-1)
f(f(x))=kn*k2*x(n2+2n+1)/(n+1)(n+2)
f(x)=k/(n+1)*x(n+1), f(f(x))=k*k*kn/((n+1)(n+1)*(n+1))*x(n+1)*(n+1)
f(f(x))=kn*k2*x(n2+2n+1)/(n+1)(n+2)
Damit wurde gezeigt, daß r(x) für dieses Beispiel graphisch richtig ermittelt wurde!
Ist dies alles richtig? Bert Wichmann!