Aufgabe:
Gegeben ist der Graph der zweiten Ablei-
tung f" einer Funktion \( f \) (Fig. 1). Welche der fol-
genden Aussagen sind wahr? Begründen Sie.
a) \( f^{\prime} \) ist streng monoton zunehmend.
b) Der Graph von \( f^{\prime} \) hat einen Wendepunkt an der Stelle \( x=0 \)
c) Der Graph von \( f \) ist für \( x>0 \) linksgekrümmt.
d) Der Graph von \( f^{\prime} \) ist für \( x>0 \) linksgekrümmt.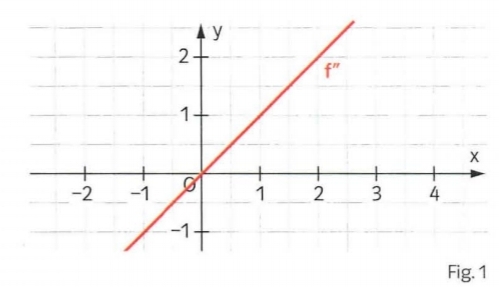
Kann mir bitte jemand bei c) und d) helfen?
Bei c) ist nach f(x) gefragt, f'(x) ist eine Parabel. Wie finde ich aus der Parabel f(x) heraus? Also wie zeichne ich den Graphen " rückwärts"?
Nun mein Problem mit d):
Ich hätte gesagt, die Aussage stimmt, weil der Graph von f'(x) eine nach oben geöffnete Parabel ist und somit an jedem Punkt linksgekrümmt ist.
In den Lösungen steht : d) Richtig. Um Aussagen über das Krümmungsverhalten von \( \mathrm{f}^{\prime} \mathrm{zu} \) machen, betrachtet man die zweite Ableitung von \( f^{\prime} \), also \( f^{\prime \prime \prime} . \) Da \( f^{\prime \prime} \) eine lineare Funktion mit positiver Steigung ist, gilt: \( f^{\prime \prime \prime}(x)>0 \) für alle \( x, \) also ist \( f^{\prime} \) für alle \( x \) linksgekrümmt.
WARUM? Warum muss ich die dritte Ableitung machen?! Es ist doch nach der Krümmung beim Graphen f' gefragt. Der Graph von f''' sieht doch ganz anders aus.
F''' ist eine Gerade mit Steigung 1, die bei y=1 liegt. Eine Gerade hat keine Krümmung. Dann kann wenn überhaupt nach der Argumentation f' gar keine Krümmung haben, was falsch ist weil f' eine linksgekrümmte Parabel ist. Oder nicht?
Liebe Grüße