Aufgabe:
Hallo, ich habe eine Schachtel ohne Deckel gegeben (siehe Skizze). Die Maße 6 und 10 Längeneinheiten sind bekannt. Die sich ergebende Kantenhöhe x unbekannt bzw. gesucht. X soll jedoch so gewählt werden, dass sich ein Schachtelvolumen von V = 30 Volumeneinheiten ergibt.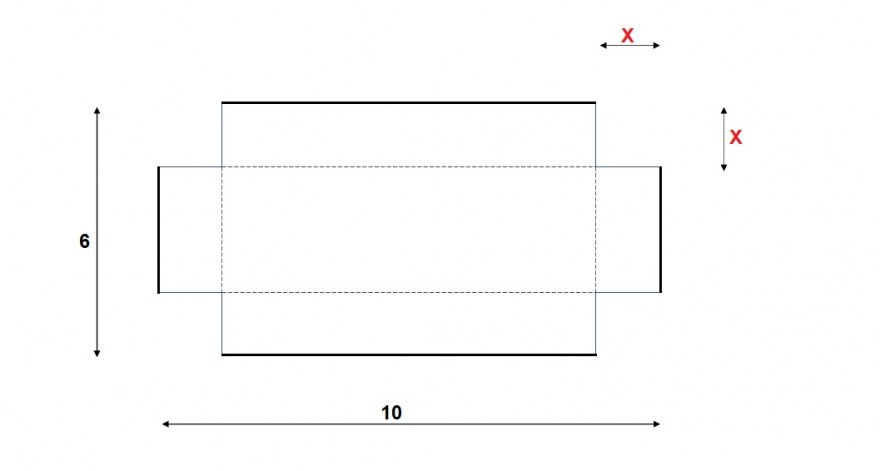
Text erkannt:
11
Problem/Ansatz:
Der Ansatz ist ja über die Volumenformel: V = 30 = (10 - 2x) (6 - 2x) x = 4x^3 - 32x^2 + 60x. Nur bin ich hier überfragt, wie ich ohne "Raten" und nur mit händischen Methoden nach x auflösen soll.
Ein weiterer Ansatz von mir war es eine Zielfunktion über V und A (A = 60 - 4x^2) aufzustellen.
Heißt: 30 = 4x^3 - 32x^2 + 60x nach x^2 aufzulösen und in A = 60 - 4x^2 einzusetzen. Und dann halt nach dem Schema einer Extremwertaufgabe weiterzurechnen. Also das x über A'(x) zu bestimmen. Jedoch kam ich auch so nicht auf die geforderten 30 VE.
Falls jemand ein Lösungsweg weiß, würde ich mich über eine Antwort freuen. Hänge nun gefühlt eine Ewigkeit an der Aufgabe.
mfg