Wie lautet der Absolutwert der Teststatistik?

Question

Aufgabe:

Text erkannt:

Eine Fabrik produziert Kugellager. Diese Kugellager sollen alle den gleichen Umfang von $10 \mathrm{cm}$ aufweisen. Bei der Weiterverarbeitung wurde jedoch festgestellt, dass der Umfang mancher Kugellager niedriger als der Sollwert $\mu_{0}=10$ ist. Daher wurde eine Stichprobe genommen und von 19 Kugellagern der Umfang nachgemessen. Die Stichprobe ergab folgenden Mittelwert: 9.77 .
Versuchen Sie (statistisch) nachzuweisen, dass der Umfang der Kugellager im Mittel niedriger als der Sollwert $\mu_{0}=10$ ist (Alternativhypothese). Nehmen Sie dabei an, dass der Umfang der Kugellager eine normalverteilte Zufallsvariable mit einer Varianz $\sigma^{2}=0.22 \mathrm{cm}^{2}$ ist. Verwenden Sie ein Signifikanzniveau von $\alpha=5 \%$.
Wählen Sie das Hypothesenpaar aus, das der Fragestellung entspricht.
##ANSWER1##
Wie lautet der Absolutwert der Teststatistik?
##ANSWER2##
Wie lautet der Absolutbetrag des kritischen Wertes?
##ANSWER3##
Wie lautet der entsprechende p-Wert gerundet auf drei Kommastellen?
##ANSWER4##
О a.1. $H_{0}: \mu \leq 10, H_{1}: \mu>10$
$\bigcirc$ a.2. $H_{0}: \mu=10, H_{1}: \mu \neq 10$
a.3. $H_{0}: \mu \geq 10, H_{1}: \mu<10$

Text erkannt:

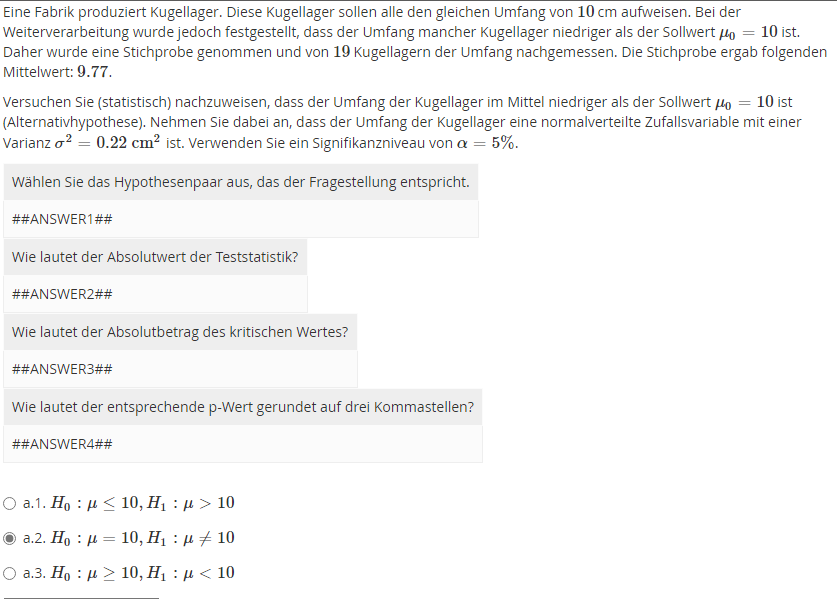
Eine Fabrik produziert Kugellager. Diese Kugellager sollen alle den gleichen Umfang von $10 \mathrm{cm}$ aufweisen. Bei der Weiterverarbeitung wurde jedoch festgestellt, dass der Umfang mancher Kugellager niedriger als der Sollwert $\mu_{0}=10$ ist. Daher wurde eine Stichprobe genommen und von 19 Kugellagern der Umfang nachgemessen. Die Stichprobe ergab folgenden Mittelwert: 9.77 .
Versuchen Sie (statistisch) nachzuweisen, dass der Umfang der Kugellager im Mittel niedriger als der Sollwert $\mu_{0}=10$ ist (Alternativhypothese). Nehmen Sie dabei an, dass der Umfang der Kugellager eine normalverteilte Zufallsvariable mit einer Varianz $\sigma^{2}=0.22 \mathrm{cm}^{2}$ ist. Verwenden Sie ein Signifikanzniveau von $\alpha=5 \%$.
Wàhlen Sie das Hypothesenpaar aus, das der Fragestellung entspricht.
##ANSWER1 ##
Wie lautet der Absolutwert der Teststatistik?
##ANSWER2##
Wie lautet der Absolutbetrag des kritischen Wertes?
##ANSWER3##
Wie lautet der entsprechende p-Wert gerundet auf drei Kommastellen?
##ANSWER4##
a.1. $H_{0}: \mu \leq 10, H_{1}: \mu>10$
\odot a.2. $H_{0}: \mu=10, H_{1}: \mu \neq 10$
a.3. $H_{0}: \mu \geq 10, H_{1}: \mu<10$

Problem/Ansatz:

1) Ich habe die a2 gewählt, weil mir das am besten vor kam.

2) (9,77-10)/Wurzel(0,22/19) = -2,1374

3) (10-9,77)/Wurzel0,22 = 0,49

4) 0,49 in Tabelle = 0,688

Alles oder nur eine Teilaufgabe ist Falsch. Ich wäre dankbar auf jede Nützliche Hilfe.

Comments

Versuchen Sie (statistisch) nachzuweisen, dass der Umfang der Kugellager im Mittel niedriger als der Sollwert μ0=10 ist (Alternativhypothese).

Das Mittel soll niedriger sein als 10. Warum nimmst du also nicht das Hypothesenpaar a.3 ?

---

ich habe alle 3 Varianten ausprobiert