Hallo,
berechne die Fläche \(F\) des Dreiecks \(F \approx 23,9\) und multipliziere das mit dem Skalarprodukt aus dem Normalenvektor \(n\) der Fläche mit dem Geschwindigkeitsvektor \(v\).
Der Normalenvektor muss normiert sein, also \(|n|=1\) $$\dot V = F \cdot \left< v, n\right> = 143 $$Bem.: der Volumenstrom \(\dot V\) ist vorzeichenbehaftet. Die 'Richtung' der Fläche wird durch \(n\) definiert. Ist \(\dot V \lt 0\) so fließt die Flüssigkeit in die Gegenrichtung zu \(n\).
Sind \(a\) und \(b\) zwei Vektoren, die das Dreieck aufspannen, so ist die Fläche $$F = \frac 12 |a \times b|$$ und $$n = \frac{a \times b}{|a \times b|}$$ Somit ist auch $$\dot V = F \cdot \left< v, n \right> = \frac 12 \left< (a \times b), \, v \right>$$
Stell Dir das Dreieck um den Vektor \(v\) verschoben vor. Das Volumen, das dabei überstrichen wird, ist das gesuchte Volumen pro Zeiteinheit:
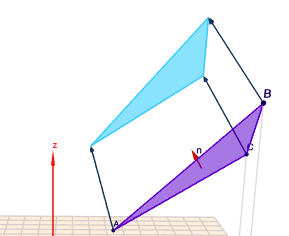
(klick auf das Bild)