Schneidewinkel von Tangenten berechnen?

Question

Aufgabe:

Gegeben ist die Funktion f(x) = |x^2 -1|.

a)  Bestimmen Sie f′(x) and ihren maximalen Definitionsbereich.

b)  Mit welchen Winkel schneiden sich die Tangenten an die Funktion f(x) bei den Stellen x=−2 und x=2?

Problem/Ansatz:

a konnte ich lösen, die Ableitung ist 2x*(x^2-1) / (|x^2-1|) und daher ist der Definitionsbereich alle reellen Zahlen außer 1. Aber b verstehe ich nicht.
Warum hat eine Tangente einen Schnittwinkel, wenn sie genau an einem Punkt die Funktion berührt? Soll ich zwei Winkel oder einen herausfinden? Oder haben beide Tangenten den gleichen Winkel? Oder ist gemeint, dass die zwei Tangenten sich irgendwo im Raum treffen und man soll diesen Schnittpunkt mit dem Winkel herausfinden? Ich weiß auch nicht, wie ich das rechnen sollte, wenn das so gemeint ist.

Answer 1

und daher ist der Definitionsbereich alle reellen Zahlen außer 1.

Da hast du vergessen, eine weitere nicht erlaubte Zahl auszuschließen.

Oder ist gemeint, dass die zwei Tangenten sich irgendwo im Raum treffen und man soll diesen Schnittpunkt mit dem Winkel herausfinden?

Sage nicht "Raum", sondern "Ebene", dann hast du es erfasst.

Comments

Okay danke und stimmt, ich hab -1 vergessen.
Wie berechne ich jetzt den Schnittpunkt dieser Tangenten? Ich weiß, dass die die Form kx+d haben müssen. f(-2) und f(2) der Tangenten ergeben -4 und 4. Aber da fehlt mir noch ein d, oder? Von wo bekomme ich das?

---

Das d interessiert kein Schwein. Nach den Koordinaten das Schnittpunkts ist nicht gefragt.

Wenn du irgendwie herausbekommen solltest, unter welchen Winkel jede Tangente die x-Achse schneidet - könntest du dann auch rausbekommen, unter welchem Winkel die y-Achse geschnitten wird?

---

Ich hab das ja nicht herausbekommen, ich möchte Funktionswerte für die beiden Tangenten haben, damit ich da dann auf einen Schnittpunkt kommen kann.

---

b)  Mit welchen Winkel schneiden sich die Tangenten an die Funktion f(x) bei den Stellen x=−2 und x=2?

damit ich da dann auf einen Schnittpunkt kommen kann.

DU BRAUCHST IHN NICHT UND AUFGABE b) VERLANGT IHN NICHT!

---

Was du tun musst, ist in dieser Reihenfolge folgendes:

Anstieg der Tangente? (Stichwort: Ableitung)

Wenn Anstieg bekannt ist: Anstiegswinkel?

(Er tritt im Steigungsdreieck der Geraden auf und ist gleichzeitig auch Schnittwinkel mit der x-Achse)

Dann: Schnittwinkel mit der y-Achse?

Dann: Schaffst du es, den "mal 2" zu rechnen?

---

Dann keine Ahnung, wie das gehen soll, sorry

---

Scheiterst du am ersten Schritt?

---

Ich hab den Anstieg der Tangenten ja schon, 4 und -4.
Wie soll ich von da auf einen Winkel kommen?

---

Rechne in dem abgebildeten rechtwinkligen Steigungsdreieck die Größe des eingezeichneten Winkels aus.

---

Noch immer keine ahnung, wie das gehen soll.
Hab jetzt -2 und 2 in die Stammfunktion eingesetzt, damit ich die Punkte P1(-2|3) und P2(2|3) kriege. Daraus habe ich dann die lineare Gleichung 3 = -4 * -2 bzw. 2 + d gemacht und bei beiden ist -5 für d rausgekommen.
Daher liegt der Schneidepunkt bei (0|5). Von -2|3 und 2|3 auf 0|5 lässt sich ein Vektor spannen und davon hab ich jetzt mit der Formel für einen Winkel zwischen zwei Vektoren 90 Grad bekommen, was sich schön anhört.
Danke für die Hilfe dennoch.

---

Du verweigerst dich gerade einem grundlegendem Wissen der 9. Klasse.

Der Winkel, nach dem ich dich frage, ist ein Winkel in einem rechtwinkligen Dreieck, dessen Gegenkathete die Länge 4 und dessen Ankathete die Länge 1 hat.

davon hab ich jetzt mit der Formel für einen Winkel zwischen zwei Vektoren 90 Grad bekommen, was sich schön anhört.

Schön für dich. Der Schnittwinkel der beiden Tangenten ist aber etwas kleiner als 30°.

---

Danke für die Korrektur, ich habe mich beim Skalarprodukt vertan. Jetzt kommen bei mir 28.072 Grad raus.

Ich will mich nicht irgendeinem Wissen verweigern, ich verstehe nur nicht, wieso Du diese Schritte anwendest und wieso Du ohne Steigungsfunktion auskommst. Ich bin froh, dass ich irgendeine Lösung verstanden habe und angesichts meines Zeitdrucks werde ich es dabei auch belassen.

Vielen ehrlichen Dank für die Bemühungen, es hat mir durchaus geholfen!

Answer 2

Gegeben ist die Funktion f(x) = |x^2 -1|.
Ich würde wie folgt vorgehen

a)  Bestimmen Sie f′(x) and ihren maximalen Definitionsbereich.

x^2 ist eine Parabel
x^2 - 1 ist eine nach unten verschobene Parabel
| x^2 - 1 | ist eine Betragsfunktion für die gilt. Bei
x^2 - 1 ≥ 0
x^2 ≥ 1
x ≥ 1
und
x ≤ -1
an den Stellen x = 1 und x =-1 wechselt die
Betragsfunktion. An diesen Stellen ist die
die Funktion nicht differenzierbar
D von f ´ = ℝ \ 1 und -1

Es gilt dafür | x^2 - 1 | = x^2 - 1. Da x = 2 sein soll
gilt als 1.Ableitung
f ´( x ) = 2x
f ´( 2 ) = 4

Die Parabel ist achsensymmetrisch zur y-Achse
Für x = -2 gilt
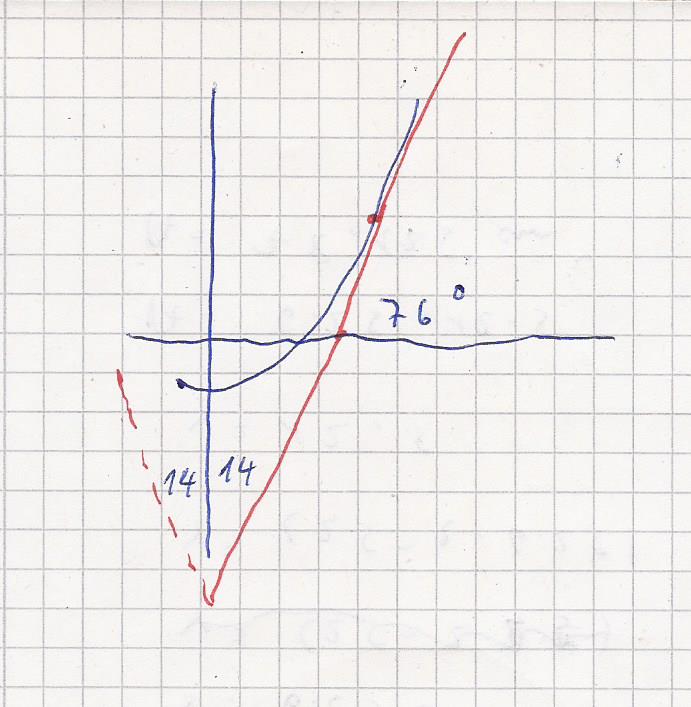
f ´( -2 ) = -4 ( siehe die Graphen )
oder
f ´( -2 ) = -4

b)  Mit welchen Winkel schneiden sich die Tangenten an die Funktion f(x) bei den Stellen x=−2 und x=2?

Die Tangenten schneiden sich aufgrund der
Symmetrie auf der y-Achse.
Die rechte Tangente hat einen
Steigungswinkel von ca 76 °.
Sie schneidet sich mit der y-Achse unter einem
Winkel von 14 ".
Die linke ebenso bzw. - 14 °
Der Schneidewinkel beträgt 2 * 14 = 28 °