Folgende Aufgabe:
In einem Spiel ist ein Ball in einem Labyrinth bestehend aus \(N\) Ringen, welche von innen nach außen von \(0\) bis \(N\) nummeriert sind. Aus dem \(k\)-ten Ring kommt man entweder auf den Ring \(k+1\) oder \(k-1\). Das Spiel ist beendet sobald der Ball entweder in Ring \(0\) angekommen ist, oder in Ring \(N\) landet, worauf der Spieler die Lust verliert weiterzuspielen und aufhört. Der Spieler bewegt den Ball mit Wahrscheinlichkeit \(\frac{1}{2}\) in den angrenzenden Ring.
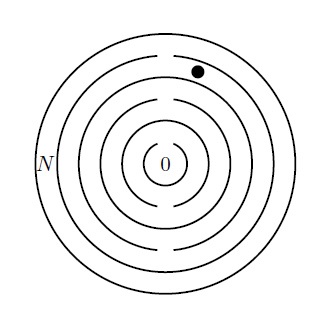
1. Beschreiben Sie das Spiel als Markovkette und geben Sie die Übergangsmatrix an.
Habe ich bereits gelöst, die Markovkette ist gegeben durch \(X_n=X_{n-1}+\xi_n\), wobei \(ℙ(\xi_n=1)=ℙ(\xi_n=-1)=\frac{1}{2}\). Die Transitionsmatrix ist entsprechend gegeben durch \(Π(i,j)=1\) wenn \(i=j \in \{0, N\}\), sonst \(\frac{1}{2}\) wenn \(j\in\{i-1,i+1\}\), \(0\) sonst.
2. Beweisen Sie, dass für jedes \(x\in\{0,\dots,N\}\) der Grenzwert \(h(x):=lim_{n\to \infty} ℙ(X_n=0|X_0=x)\) existiert und zeigen Sie, dass \(h(x)=\sum_{y=0}^N Π(x,y) h(y)\)
Hier stecke ich leider fest. Die Definition von \(h(x)\) lädt eigentlich gerade dazu ein, einen Induktionsbeweis zu nutzen, aber irgendwie kommt da nichts gescheites bei rum. Außerdem weiß ich nicht, wie ich zeigen soll, dass der Grenzwert existiert. Intuitiv ist das natürlich klar, dass das gilt aber ich weiß nicht wie ich es mathematisch korrekt zeige.