Ich habe eine Frage bezüglich folgender Aufgabe:
Sind die folgenden Vektoren linear unabhängig, d.h. spannen Sie jeweils einen Vektorraum der Dimension 3 auf?
Begründen Sie.
Wenn die Vektoren linear abhängig sind, geben Sie die Dimension und eine Basis des Vektorraumes an.
a)
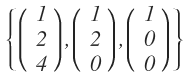
Text erkannt:
\( \left\{\left(\begin{array}{l}1 \\ 2 \\ 4\end{array}\right),\left(\begin{array}{l}1 \\ 2 \\ 0\end{array}\right),\left(\begin{array}{l}1 \\ 0 \\ 0\end{array}\right)\right\} \)
b)
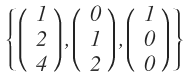
Text erkannt:
\( \left\{\left(\begin{array}{l}1 \\ 2 \\ 4\end{array}\right),\left(\begin{array}{l}0 \\ 1 \\ 2\end{array}\right),\left(\begin{array}{l}1 \\ 0 \\ 0\end{array}\right)\right\} \)
Antwort:
a)
Hier habe ich die Determinante berechnet, welche ungleich 0 ist. Die Vektoren sind somit linear unabhängig.
Ist das die Lösung? Was meinen die mit "spannen Sie jeweils einen Vektorraum der Dimension 3 auf"?
b)
Hier habe ich mit dem Gauß-Verfahren die letzte Zeile auf 0 bringen können. Die Vektoren sind hier also linear abhängig.
Wie gebe ich jetzt die Dimension und eine Basis des Vektorraumes an?
Ich bedanke mich im voraus für alle Antworten :)