Im Quadrat ABCQ1 schneidet die Mittelparallele m1 zwischen AQ1 und BC die Diagonale AC=w1 in P1. w2 sei die Halbierende des Winkels ABC und m2 sei die Mittelparallele zwischen m1 und BC, dann schneiden sich w2 und m2 in P2.
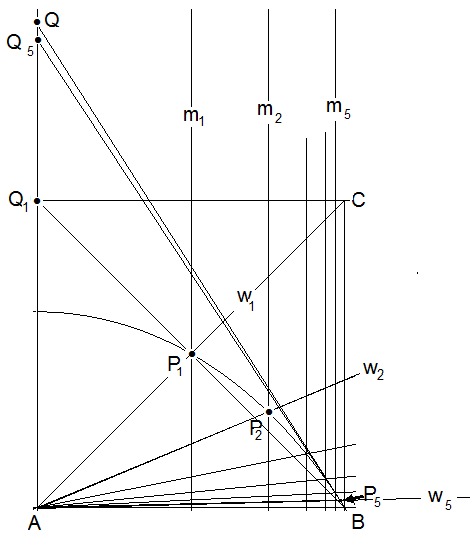
Allgemein ist mi die Mittelparallele zwischen mi-1 und BC und wi die Winkelhalbierende zwischen AB und wi-1. mi und wi schneiden sich in Pi. In der Graphik sind die Punkte P1 bis P5 dargestellt. Die Gerade BPi scheidet die Gerade AQ1 in Qi.
Bestimmen Sie lim(Qi) für i gegen Unendlich.