Extremwertaufgaben Gymnasium Q1

Question

Aufgabe:

ist keine Buch Fotografie!!

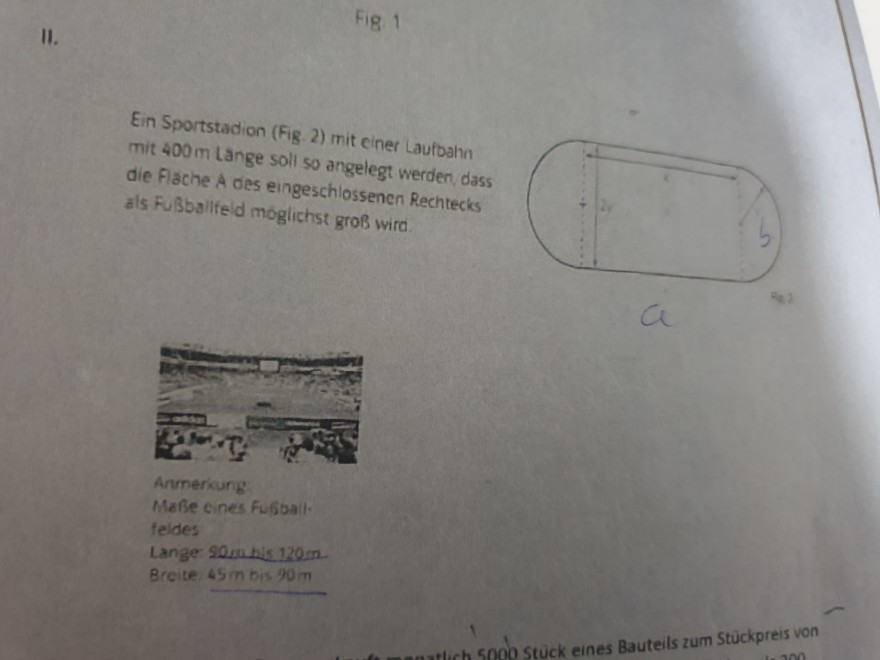
Text erkannt:

\( 11 . \)
Ein Sportstadion (Fig. 2) mit einer Laufbahn mit \( 400 \mathrm{~m} \) Lange soll so angelegt werdinn die Flache A des eingeschiocegt werden, das als Fußballfeld moglichst ossencn
Mafe cines feldes Lange: SOsubls. Breite \( 45 m \) bis \( 90 \mathrm{~m} \)

Text erkannt:

9

Habe Montag Klausur trotz Corona und lerne schon seit 2 Wochen dafür.

Eigentlich dachte ich ,dass ich Extremwertaufgaben kann aber die hier leider nicht...!
Problem/Ansatz:

Answer 1

$$A(r)=2r*(400-2πr)/2$$

$$A(r)=r*(400-2πr)$$

$$A(r)=-2πr^2+400r$$

$$A'(r)=-4πr+400$$

$$A''(r)=-4π$$

$$r=100/π≈31,831 m$$

$$b≈63,662$$

$$a=100 m$$

$$A(63,662)≈6366,2. m^2$$

Es wurde hier aber als Länge die Innenkante genommen, da keine Laufbahnbreite angegeben war.

Doch es ist ja auch ein gutes Ergebnis, dass wir eine 100 m Bahn haben.

Answer 2

Das Fußballfeld habe die Breite 1x und die Länge a. Dann lautet die Hauptbedingung A(x)=2x·a und die Nebenbedingung 2πx+2a=400 oder a=200-πx.

Nebenbedingung in Hauptbedingung einsetzen: A(x)=2x·(200-πx)=400x-2πx². Nullstelle der ersten ist der Radius des gewünschten Halbkreises. Damit dann Länge und Breite berechnen.