Aufgabe: Extremwertaufgabe
Kann mir vielleicht jemand von euch die Aufgaben berechnen und mir versuchen zu erklären wie ihr das gemacht habt?
LG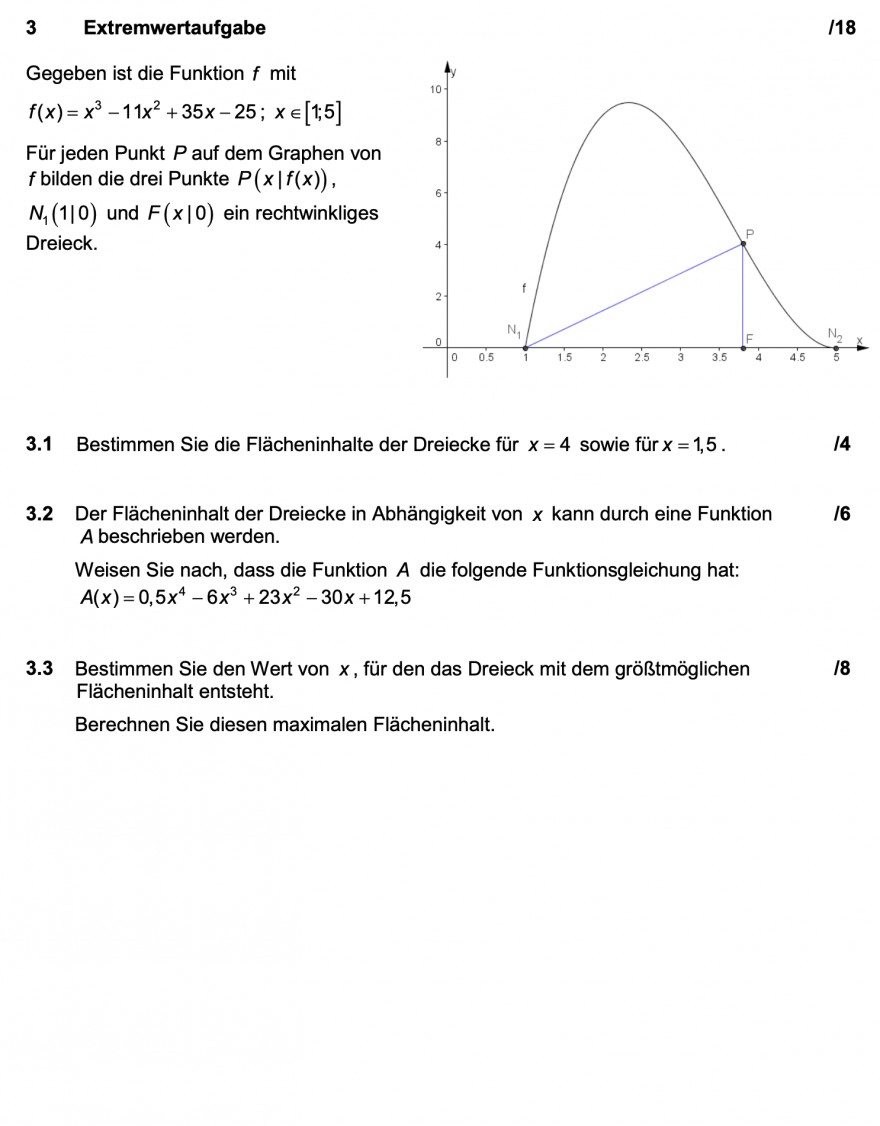
Text erkannt:
\( 3 \quad \) Extremwertaufgabe
Gegeben ist die Funktion \( f(x)=x^{3}-11 x^{2}+35 x-25 ; x \in[1 ; 5] \)
Für jeden Punkt \( P \) auf dem Graphen von \( f \) bilden die drei Punkte \( P(x \mid f(x)) \)
\( N_{1}(1 \mid 0) \) und \( F(x \mid 0) \) ein rechtwinkliges Dreieck.
3.1 Bestimmen Sie die Flächeninhalte der Dreiecke für \( x=4 \) sowie für \( x=1,5 \). 14
3.2 Der Flächeninhalt der Dreiecke in Abhängigkeit von \( x \) kann durch eine Funktion 16
A beschrieben werden.
Weisen Sie nach, dass die Funktion \( A \) die folgende Funktionsgleichung hat:
\( A(x)=0,5 x^{4}-6 x^{3}+23 x^{2}-30 x+12,5 \)
3.3 Bestimmen Sie den Wert von \( x \), für den das Dreieck mit dem größtmöglichen /8 Flächeninhalt entsteht.
Berechnen Sie diesen maximalen Flächeninhalt.