Aufgabenstellung:
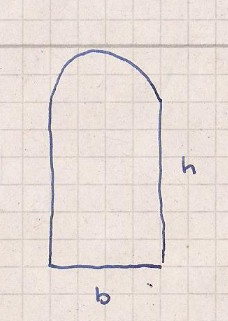
Die Geometrie eines Kirchenfensters (Halbkreis und Rechteck, s. Abbildung) soll konstruiert werden.
Der Umfang ist mit U = Uo festgelegt. Die Maße des Fensters sind so zu wählen, das die Flache maximal wird, um möglichst viel Licht in die Kirche zu leiten.
Lösen Sie folgende Teilaufgaben:
a) Stellen Sie die Zielfunktion, die Nebenbedingung sowie die Lagrangesche Hilfsfunktion L auf!
b) Berechnen Sie die zur Optimierung notwendigen Gleichungen!
(Hinweis: Das Gleichungssystem muss nicht gelost werden.)
\(\displaystyle \quad f(b, h)=b \cdot h+\frac{\pi b^{2}}{8} \)
Unter Nebenbedingung \( b\left(1+\frac{\pi}{2}\right)+2h=U_{0} \)
Nebenbedingungen:
\(\underbrace{b \cdot\left(1+\frac{\pi}{2}\right)+2 h-U_{0}}_{g(b, h)}=0\)
\( {\text {Lagrange-Funktion }} \mathscr{L}(b, h, \lambda)=f(b, h)+\lambda g(b, h) \)
\(\begin{aligned} \mathscr{L}(b, h, h) & =b \cdot h+\frac{\pi b^{2}}{8}+\lambda\left[b\left(1+\frac{\pi}{2}\right)+2 h-U_{0}\right] \\ & =b h+\frac{\pi b^{2}}{8}+h b\left(1+\frac{\pi}{2}\right)+2 \lambda h-\lambda U_{0} \end{aligned}\)
Ableitungen
\(\begin{array}{l} \mathscr{L}_{b}=h+\frac{\pi b}{4}+\lambda\left(1+\frac{\pi}{2}\right) \\[8pt] \mathscr{L}_{h}=b+2 \lambda \\[8pt] \mathscr{L}_{\lambda}=b\left(1+\frac{\pi}{2}\right)+2 h-U_{0} \end{array}\)
Notwendige Bedingungen
\( \begin{array}{l} h+\frac{\pi b}{4}+h\left(1+\frac{\pi}{2}\right)=0 \\[8pt] b+2 \lambda=0 \\[8pt] b\left(1+\frac{\pi}{2}\right)+2 h-U_{0}=0 \end{array} \)
Hi... Ich wollte fragen ob einer mal drüber schauen kann und mir sagen ob alles richtig ist? Die Aufgabe ist sehr wichtig für die Klausur demnächst.