Wie wurde der Term vereinfacht?

Question

Hallo. Ich habe hier folgendes bestimmte Integral, welches ich bereits gelöst habe. Mein Ergebnis habe ich auf der Website integralrechner.de verglichen.

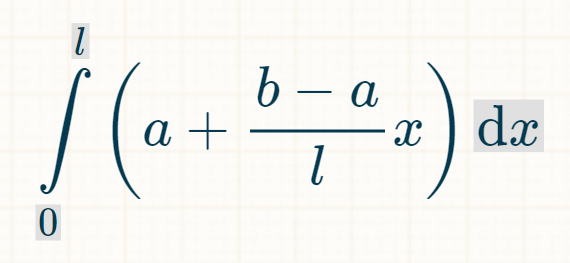
Text erkannt:

\( \int \limits_{0}^{l}\left(a+\frac{b-a}{l} x\right) \mathrm{d} x \)

Text erkannt:

\( \int \limits_{0}^{l}\left(a+\frac{b-a}{l} x\right) \mathrm{d} x \)

Ich habe folgendes Ergebnis:

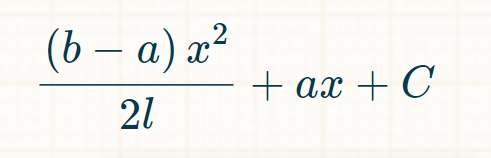
Soweit so gut. Nun kann man das auch noch etwas vereinfacht darstellen. Hierfür hat mir der Integralrechner folgendes Ergebnis geliefert.

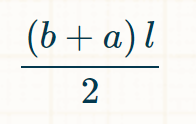
Text erkannt:

\( \frac{(b+a) l}{2} \)

Mit der Anmerkung:

Text erkannt:

Beachte: Das bestimmte Integral wurde unter Zuhilfenahme der Symmetrie der Funktion bestimmt.

Kann mir bitte jemand schrittweise erklären, wie es hier vereinfacht wurde?

Ich weiß dass es verschiedenste Vereinfachungen gibt. So hab ich z.B. einfach nur das "a" ausgeklammert, weiter wüsste ich nicht wie ich vereinfachen soll. Ist natürlich immer Ansichtssache aber wie hat hier die Symmetrie der Funktion beigeholfen.

Danke für Eure Mühen.

Text erkannt:

\( \frac{(b-a) x^{2}}{2 l}+a x+C \)

Comments

Das erste ist die Stammfunktion, das zweite das bestimmte Integral. Was soll denn da vereinfacht worden sein? Das ist lediglich etwas umgeformt worden.

Answer 1

\( \frac{(b-a) x^{2}}{2 l}+a x+C \)

Das ist die Stammfunktion .

Setze \(l\) für \(x\) ein.

Setze \(0\) für \(x\) ein.

Subtrahiere die beiden Ergebnisse.

Comments

Danke aber das habe ich ja auch soweit schon. Vielleicht habe ich mich nicht deutlich genug ausgedrückt. Von einander subtrahiert erhalte ich:

Text erkannt:

\( =a \cdot l+\frac{b-a}{2 l} \cdot l^{2} \)
\( =l \cdot\left(a+\frac{b-a}{2}\right) d / \frac{\text { noch weiles }}{2} \cdot l / 1 \)

das schwarz unterstrichene ist das vereinfachte bestimmte Integral. Das rot markierte ist dasselbe Ergebnis, nur ein Schritt weiter vereinfacht.

Meine Frage war jetzt: wie hat man da noch weiter vereinfacht? bzw. wie ist man da vorgegangen? Danke

---

Bruchrechenregeln. Die Summanden von \(a+\frac{b-a}{2}\) Gleichnamig machen und die Regeln für die Addition von Brüchen anwenden.

Answer 2

Du hast eine Stammfunktion  F(x) bestimmt, nicht das Integral.

Rechne nun F(l) - F(0) und du bekommst:

(a+b)*l / 2  - 0 und das ist es !