Relation rekursiv, symmetrisch und transitiv? Wie interpretiere ich hier die Bedingung?

Question

Guten Tag zusammen: Wie interpretiere ich hier die Bedingung?

Ich habe folgende Aufgabe:

Sei X:= {1, 2} und R Teilmenge von P(X) x P(X) eine Relation auf der Potenzmenge P(X), definiert durch

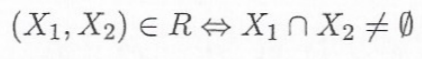
und wir sollen bestimmen ob diese Relation rekursiv, symmetrisch und transitiv ist?

Text erkannt:

\( \left(X_{1}, X_{2}\right) \in R \Leftrightarrow X_{1} \cap X_{2} \neq \emptyset \)

Mein Ansatz wäre:

P(X) = {{},{1},{2},{1,2}}

{{},{1},{2},{1,2}} x {{},{1},{2},{1,2}} = { ({},{}), ({},{1}), ({},{2}), ({},{1,2}),  ({1},{}), ({1},{1}), ({1},{2}), ({1},{1,2}),  ({2},{}), ({2},{1}), ({2},{2}), ({2},{1,2}),  ({1,2},{}), ({1,2},{1}), ({1,2},{2}), ({1,2},{1,2}) }

Ich komme nicht draus, was X₁ Schnittmenge X₂ != {} das bedeuten soll?

Weil so wie ich die Relation aufgeschrieben habe, ist sie ja rekursiv, symmetrisch und transitiv. Laut den Lösungen ist sie nur symmetrisch.

Vielen Dank im Voraus!

LG
Pfizer

Answer 1

Wie interpretiere ich hier die Bedingung?

Die Mengen X1 und X2 stehen in Relation R zueinander, wenn sie mindestens ein gemeinsames Element enthalten.

Genügt dir das so?

Comments

Guten Tag Lu

Danke vielmals für die Antwort. Leider hat es bei mir noch nicht klick gemacht. Welche Mengen sind X₁ und X₂ ?

---

"Welche Mengen sind X1 und X2 ?" Das ist zusammen (X1, X2) ein Mengenpaar aus P(X)

Das beschreibt auch: "R Teilmenge von P(X) x P(X)"

Betrachte deine Grundmenge { ({},{}), ({},{1}), ({},{2}), ({},{1,2}), ({1},{}), ({1},{1}), ({1},{2}), ({1},{1,2}), ({2},{}), ({2},{1}), ({2},{2}), ({2},{1,2}), ({1,2},{}), ({1,2},{1}), ({1,2},{2}), ({1,2},{1,2}) }

Nun R = { ({1},{1}), ({1},{1,2}), ({2},{2}), ({2},{1,2}), ({1,2},{1}), ({1,2},{2}), ({1,2},{1,2}) }

Bitte genau überprüfen.

---

Guten Tag Lu

Danke vielmals. Jetzt habe ich es verstanden. X1 und X2 sind die Elemente in der binären Relation.

LG
Pfizer