Nullstellen gesucht für f(x) = x + 2/√x

Question

Aufgabe:

Nullstellen gesucht:

\( f(x)=x+\frac{2}{\sqrt{x}} \)

\( =\frac{(\sqrt{x}-1) \cdot(x+\sqrt{x}+1)}{x^{\frac{3}{2}}} \)

\( =\frac{3}{2 \cdot x^{\frac{5}{2}}} \)

Es kommt eine Lösung raus - wieso rational? Es gibt keine rationale Nullstelle?

Comments

a) Hauptnenner bilden und Zähler Null setzen

b) Zähler Null setzen, Satz vom Nullprodukt

c) hat keine Nullstelle

Answer 1

Die Funktion f(x)=x+\( \frac{2}{\sqrt{x}} \) hat keine reellen Nullstellen.

Ihre Ableitung f '(x)=1-\( \frac{1}{x^{3/2}} \) hat die Nullstelle x=1.

Ihre Stammfunktion F(x)=\( \frac{x^2}{2} \)+4√x hat die Nullstelle x=0.

Answer 2

Text erkannt:

\( f(x)=x+\frac{2}{\sqrt{x}}=\frac{x \cdot \sqrt{x}+2}{\sqrt{x}} \)
\( f(x)=0 \)
\( x \cdot \sqrt{x}+2=0 \)
\( x \cdot \sqrt{x}=-\left.2\right|^{2} \)
\( x^{3}=4 \)
\( x=4^{\frac{1}{3}} \)
Quadrieren ist keine Äquivalenzumformung darum:
Probe durch Einsetzen in \( f(x) \) :
\( f\left(4 \frac{1}{3}\right)=4 \frac{1}{3}+\frac{2}{\sqrt{4 \frac{1}{3}}} \approx 3,17 \neq 0 \)

Text erkannt:

( \( f(x)=x+\frac{2}{\sqrt{x}} \)
\( \mathrm{g} \mid 1: x=4^{\frac{1}{3}} \)
\( \mathrm{A}= \) Schneide \( (\mathrm{f}, \mathrm{g} / 1,(1.59,3.17)) \)

Comments

WO ist der fehler genau und wie kann man es mathematisch begründen. wieso geht die gleichung auf ?

---

- 2  =  x•\( \sqrt{x} \) = x *\( x^{0,5} \)=\( x^{1,5} \)

x =   \( \sqrt[1,5]{-2} \)= \( -2^{1,5} \) → komplexe Zahl (Wolfram)

Oder so:

- 2  =  x•\( \sqrt{x} \)  = \( \sqrt{x^2• x} \) =  \( \sqrt{x^3} \)

\( \sqrt{x^3} \) = - 2

\( \sqrt{x^3} \) + 2=  0  →  Es existiert keine Lösung ∈  ℝ.

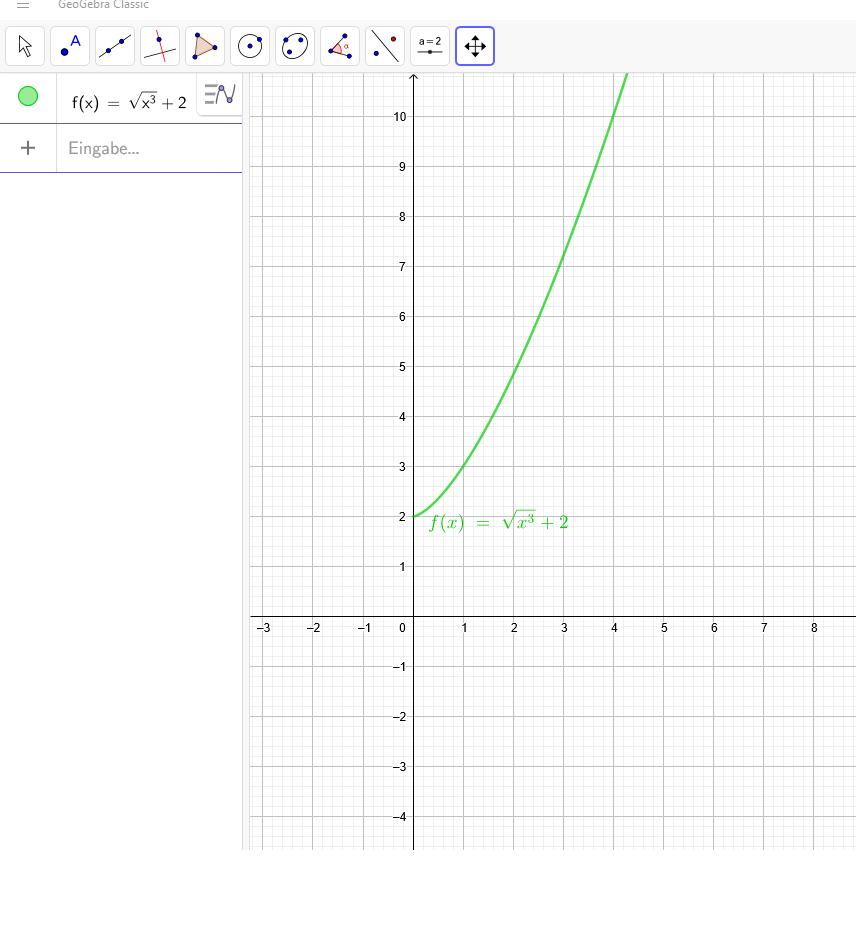
Text erkannt:

\( f(x)=\sqrt{x^{3}}+2=\Omega \)
Eingabe...