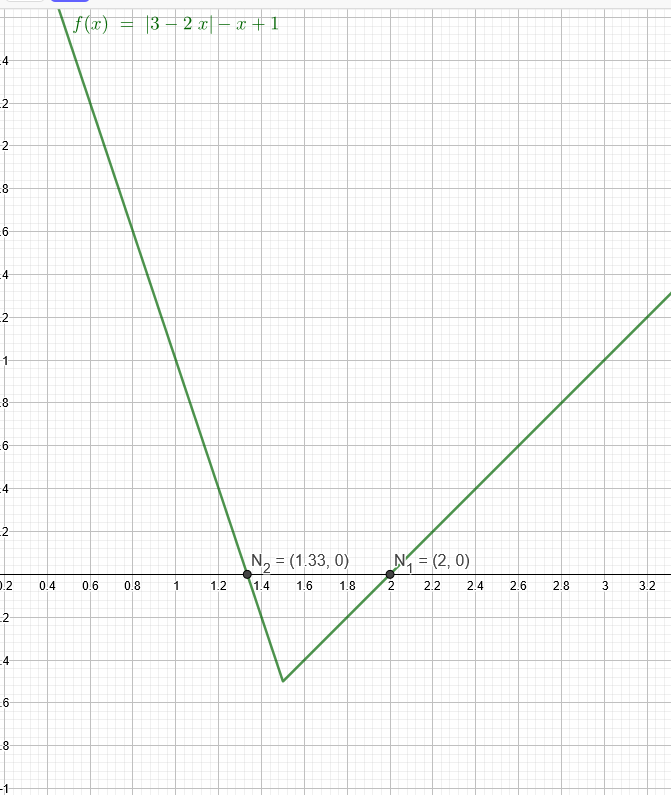
So geht es auch:
|3-2x| = x-1
\( \sqrt{(3-2x)^2} \)= x - 1
\( (3-2x)^{2} \) = \( (x-1)^{2} \)
9-12x+4\( x^{2} \)=\( x^{2} \)-2x+1
3\( x^{2} \)-10x=-8
\( x^{2} \)-\( \frac{10}{3} \)x=-\( \frac{8}{3} \)
(x-\( \frac{5}{3} \))^2=-\( \frac{8}{3} \)+\( \frac{25}{9} \)=\( \frac{1}{9} \)
x₁=\( \frac{5}{3} \)+\( \frac{1}{3} \)=2
x₂=\( \frac{5}{3} \)-\( \frac{1}{3} \)=\( \frac{4}{3} \)