Aufgabe: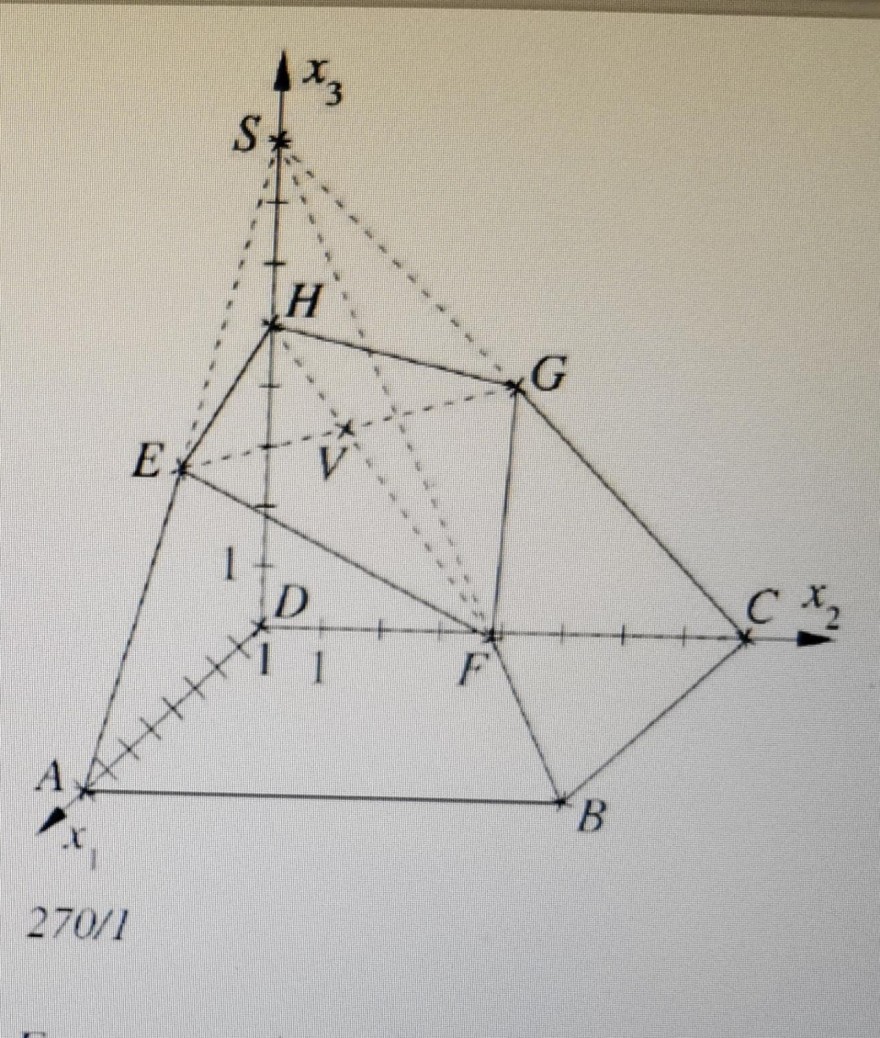
Ein Designer erhält von einer Süßwarenfirma den Auftrag, eine neue Schachtel für ihre Schokolinsen zu entwerfen. Der Entwurf sieht vor, dass die Schachtel Teil einer Pyramide mit quadratischer Grundfläche ist. Durch den Schnitt mit einer geeigneten Ebene entsteht als Schnittfläche die viereckige Deckfläche der Schachtel. Im verwendeten kartesischen Koordinatensystem hat die Grundfläche der Pyramide die Eckpunkte A(8I0I0), B(8I8I0), C(0I8I0), D(0I0I0), ihre Spitze ist der Punkt S(0I0I8).
Die Schnittebene Eegh wird festgelegt durch die Punkte E(4I0I4), G(0I4I4), und H(0I0I5) (alle Angaben sind in cm). Die Schachtel ist dann der Körper mit den Eckpunkten A,B,C,D,E,F,G,H.
Problem/Ansatz:
a) Geben Sie eine Parametergleichung der Ebene an und bestimmen Sie eine Koordinatengleichung dieser Ebene. (Zur Kontrolle:Eegh: x₁+x₂+4*x₃+20 )