Wahrscheinlichkeit , 90% Sicherheit

Question

Hallo Mathe fans!

Hier die Aufgabe, wie rechnet man sowas, ein ereignis tritt mit eine Wahrscheinlichkeit von 1 zu 20 auf es soll mit eine 90% sicherheit diese ereignis zutreffen, wieviele versuche sind dann notwendig?

Gruß João

Answer 1

Hallo João,

 

das Ereignis hat die Wahrscheinlichkeit 1 zu 20, also p = 0,05.

Die Gegenwahrscheinlichkeit, also die Wahrscheinlichkeit, dass das Ereignis nicht eintritt, beträgt demnach

1 - p = 0,95.

 

P(Ereignis tritt nicht ein bei einem Versuch) = 0,95¹

P(Ereignis tritt nicht ein bei zwei Versuchen) = 0,95²

P(Ereignis tritt nicht ein bei drei Versuchen) = 0,95³

usw.

 

Bei wieviel Versuchen ist also die Wahrscheinlichkeit, dass das Ereignis nicht eintritt, kleiner oder gleich 10%?

0,95ⁿ ≤ 0,1

n = ln(0,1)/ln(0,95) ≈ 44,89

 

Man muss den Versuch also 45 mal ausführen, um mit einer Wahrscheinlichkeit von (mehr als) 90% das Ereignis zu erhalten.

 

Probe:

0,95⁴⁴ ≈ 0,1047 | Es tritt also mit einer W. von mehr als 10% das Ereignis in 44 Versuchen nicht ein.

0,95⁴⁵ ≈ 0,0994 | Es tritt also mit einer W. von weniger als 10% das Ereignis in 45 "jedesmal nicht" ein.

 

Besten Gruß

Comments

Sehr gerne; ich hoffe, ich konnte helfen :-)

---

Hallo Brucybabe, was ich nicht ganz verstehe ist warum du mit der Gegenwahrscheinlichkeit rechnen und nicht mit Wahrscheinlichkeit die es zutrifft? ansonsten habe ich verstanden

Gruß João

---

Ich nahm die Gegenwahrscheinlichkeit, weil das den Rechenaufwand enorm verringert - mehr dazu heute Abend, bin unterwegs. Brucybabe

---

Hallo João,

 

um mein Vorgehen deutlich zu machen, habe ich einmal ein Baumdiagramm für 3 Durchgänge des Versuchs erstellt:

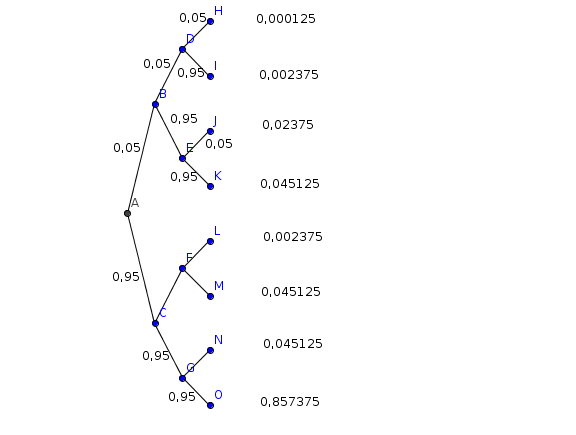
Es sind hier 8 mögliche Folgen der ersten drei Versuche skizziert - hier nenne ich das Eintreten des Ereignisses 1 und das Nichteintreten des Ereignisses 0 - 

P(000) = 0,95 * 0,95 * 0,95 = 0,857375

P(001) = 0,95 * 0,95 * 0,05 = 0,045125

P(010) = 0,95 * 0,05 * 0,95 = 0,045125

P(011) = 0,95 * 0,05 * 0,05 = 0,002375

P(100) = 0,05 * 0,95 * 0,95 = 0,045125

P(101) = 0,05 * 0,95 * 0,05 = 0,002375

P(110) = 0,05 * 0,05 * 0,95 = 0,002375

P(111) = 0,05 * 0,05 * 0,05 = 0,000125

In den blau markierten Abfolgen tritt das Ereignis (mindestens einmal) ein; die Summe dieser Wahrscheinlichkeiten beträgt 0,142625 = 14,2625%

Ein ziemlicher Rechenaufwand, nicht wahr?

Wir hätten auch ständig die Summe kontrollieren müssen, um zu sehen, ob wir auf mehr als 90% Wahrscheinlichkeit für das Eintreten des Ereignisses kommen.

Wenn ich aber 1 - Gegenwahrscheinlichkeit = 1 - 0,857375 rechne, komme ich auch auf 0,142625.

 

Aus diesem Grunde rechnet man im Allgemeinen bei Aufgaben mit "P(mindestens einmal)" mit

1 - P("keinmal").

 

Siehe auch zum Beispiel die Antworten vom Mathecoach und von JotEs auf die Frage

https://www.mathelounge.de/48200/wurfel-geworfen-werden-wahrscheinlichkeit-sechs-wurfeln

 

Besten Gruß

---

Vielen Dank Brucybabe, ich denke jetzt habe ich es verstanden!

super erklärung!!!

Gruß João

PS: ich habe gelesen du bist Dipl.-Psychologe , kannst du mir ein gutes buch empfehlen über verhaltensforschung, Danke.

---

Hallo João,

freut mich sehr, dass Du es verstanden hast!

Was Psychologie-Literatur anbelangt, bin ich nicht mehr auf dem Laufenden - wenn Du etwas Spezielles zur Verhaltensforschung suchst (für Schule oder Universität) wäre es am besten, Du fragst einen Lehrer oder Professor nach einem guten Buch.

Allgemein kann ich nur sagen, dass englischsprachige Literatur (vornehmlich aus den USA) wesentlich besser ist als deutschsprachige.

Ein Buch, was sich mit Evolution (auch des Verhaltens) befasst, und was ich als einziges freiwillig mehrmals gelesen habe (!), ist

Richard Dawkins: Das egoistische Gen

Gibt es für ca. 20 Euro zum Beispiel bei Amazon.

Besten Gruß

Andreas

---

Hallo Brucybabe,

vielen dank für den Tipp, werde mir das anschauen, ist ein Hobby von mir Psychologie und wie gesagt alles was mit Verhaltensforschung zu tun hat.

Gruß João

---

Gerne, João;

ich fand das Buch hochinteressant, ist allerdings keine leichte Kost :-)