Aufgabe:
Zoo. Ein Tiergehege wird durch einen Zaun f(x)= (4-x) * e^x/2 , einen Wassergraben und eine Mauer bei x= -4 wie abgebildet begrenzt (1 LE = 100m).
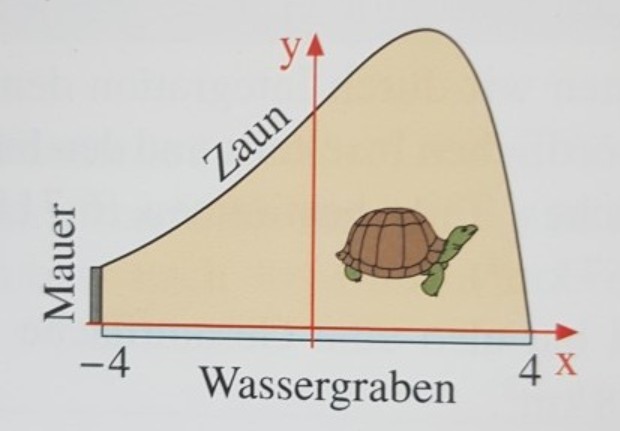
a) Wie groß ist die maximale Nord-Süd-Ausdehnung des Geheges? Wie lang ist die Begrenzungsmauer?
b) Bestimmen Sie den Parameter a so, dass F(x)= (a-2x) * e^x/2 eine Stammfunktion von f ist. Welchen Flächeninhalt hat das Gehege?
Problem/Ansatz:
Ich würde mich sehr freuen, wenn ihr mir die Ansätze nennen könntet.