Question

Bestimme die Grenzwerte lim ×->+∞ der folgenden Funktion:

1. F(x) = \( \frac{1}{4} \)e^2x  * (x² -2)

2. F(X) = e^1-x² 

Answer 1

F(x) = \( \frac{1}{4} \)\( e^{2x} \)  * (x² -2)

\( \lim\limits_{x\to\infty} \)\( \frac{1}{4} \)\( e^{2x} \)  * (x² -2)  → +∞

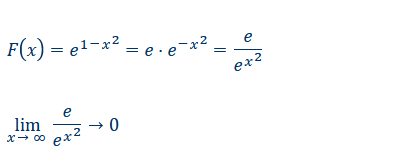
Text erkannt:

\( F(x)=e^{1-x^{2}}=e \cdot e^{-x^{2}}=\frac{e}{e^{x^{2}}} \)
\( \lim \limits_{x \rightarrow \infty} \frac{e}{e^{x^{2}}} \rightarrow 0 \)

Text erkannt:

GeoGebra Classic
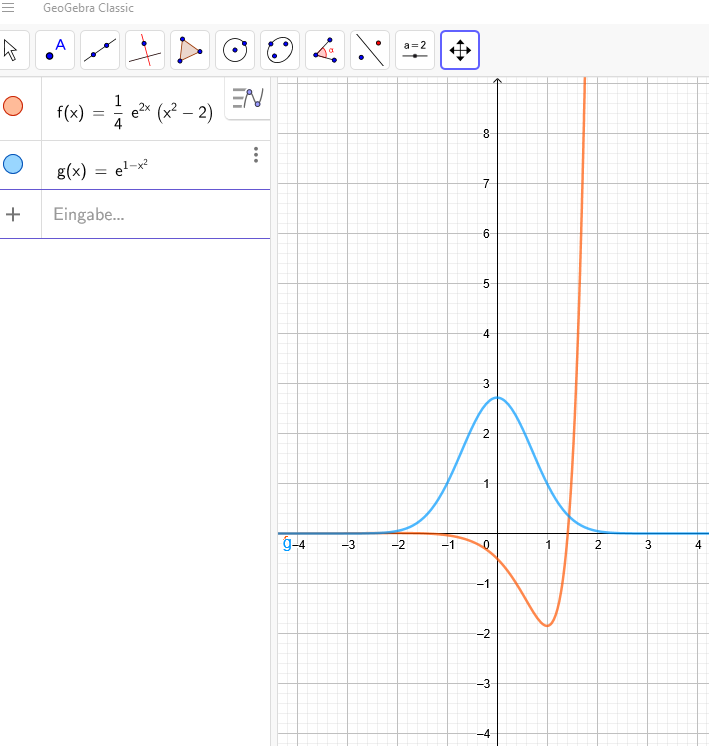
\( f(x)=\frac{1}{4} e^{2 x}\left(x^{2}-2\right) \)
\( g(x)=e^{1-x^{2}} \)
\( +\quad \) Eingabe...

Answer 2

\(\begin{aligned} &  & x & \to\infty\\ & \implies & x^{2} & \to\infty\\ & \implies & 1-x^{2} & \to-\infty\\ & \implies & e^{1-x^{2}} & \to0 \end{aligned}\)

Die andere Aufgabe wird prinzipiell genauso gelöst. Beachte dabei, dass sich in Produkten der exponentielle Teil durchsetzt.

Answer 3

Der erste ist +∞ . (Beide Faktoren werden schnell groß.)

Der zweite ist 0  ( da negativer Exponent bei e)