Hallo Alissa,
der Mittelpunkt \(P\) einer Strecke, die durch die Punkte \(A\) und \(D\) gegeben ist, berechnet sich aus
$$P = \frac 12(A+D) = \frac 12\left( \begin{pmatrix}0\\ 0\\ 0\end{pmatrix} + \begin{pmatrix}-6\\ 0\\ 0\end{pmatrix}\right) = \begin{pmatrix}-3\\ 0\\ 0\end{pmatrix}$$
Genauso ist
$$Q = \frac12(A+E) = \begin{pmatrix}-1.5\\ 0.5\\ 2.5\end{pmatrix} \\ R = \frac12(C +D) = \begin{pmatrix}-6\\ 4\\ 0\end{pmatrix}$$
Die Parameterform einer Geraden \(g\) durch zwei Punkte \(P\) und \(F\) ist
$$\begin{aligned}g: \quad \vec x &= P + s\cdot(F-P) = \begin{pmatrix}-3\\ 0\\ 0\end{pmatrix} + s\cdot \left( \begin{pmatrix}-3\\ 6\\ 5\end{pmatrix} - \begin{pmatrix}-3\\ 0\\ 0\end{pmatrix}\right) \\\vec x &= \begin{pmatrix}-3\\ 0\\ 0\end{pmatrix} + s \cdot \begin{pmatrix}0\\ 6\\ 5\end{pmatrix}\end{aligned}$$
und für die Gerade \(h\) durch die Punkte \(Q\) und \(R\) gilt das in gleicher Form:
$$h: \quad \vec x = \begin{pmatrix}-1.5\\ 0.5\\ 2.5\end{pmatrix} + t\cdot \begin{pmatrix}-4.5\\ 3.5\\ -2.5\end{pmatrix}$$
Sollten sich die Geraden schneiden, so muss es ein Paar für \(s\) und \(t\) geben, für das gilt
$$\vec g(s) = \vec h(t)$$
Daras erhält man nach dem Gleichsetzen der beiden Geraden ein überbestimmtes Gleichungssystem
$$\begin{pmatrix}-3\\ 0\\ 0\end{pmatrix} + s \cdot \begin{pmatrix}0\\ 6\\ 5\end{pmatrix} = \begin{pmatrix}-1.5\\ 0.5\\ 2.5\end{pmatrix} + t\cdot \begin{pmatrix}-4.5\\ 3.5\\ -2.5\end{pmatrix} \\ s \cdot \begin{pmatrix}0\\ 6\\ 5\end{pmatrix} + t\cdot \begin{pmatrix}4.5\\ -3.5\\ 2.5\end{pmatrix} = \begin{pmatrix}1.5\\ 0.5\\ 2.5\end{pmatrix}$$
aus der ersten Zeile folgt bereits \(t=1/3\). Setzt man das in die zweite Zeile ein, so folgt daraus \(s=5/18\). Setzt man aber zur Kontrolle das gewonnene \(t\) und \(s\) in die dritte Zeile ein,so steht dort
$$\frac{5}{18}\cdot5 + \frac 13 \cdot 2,5 = \frac{20}9\ne 2,5$$
Damit existiert keine Lösung und somit auch kein Schnittpunkt. Das ganze im Bild
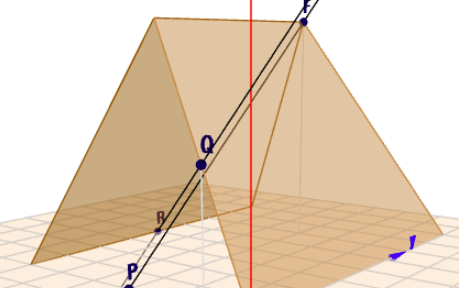
(klick auf das Bild)