Thema: steckbriefaufgaben 4. grades

Question

Eine Funktion 4. Grades verläuft symmetrisch zur y-Achse.

Der Wendepunkt ist W (2/0).

Sie geht durch den Punkt P ( 4/ 0,75).
Gesucht:  Die allgemeine Funktionsgleichung.

Answer 1

Ansatz

f(x) = ax^4 + bx^3 + cx^2 + dx + e

mit b = d = 0 wegen der Achsensymmetrie

f(x) = ax^4 + cx^2 + e

Bedingungen

f(2)=0
f''(2)=0
f(4)=0.75

Gleichungssystem

16·a + 4·c + e = 0
48·a + 2·c = 0
256·a + 16·c + e = 3/4

Errechnete Funktion

f(x) = -1/64·x^4 + 0,375·x^2 - 1,25

Answer 2

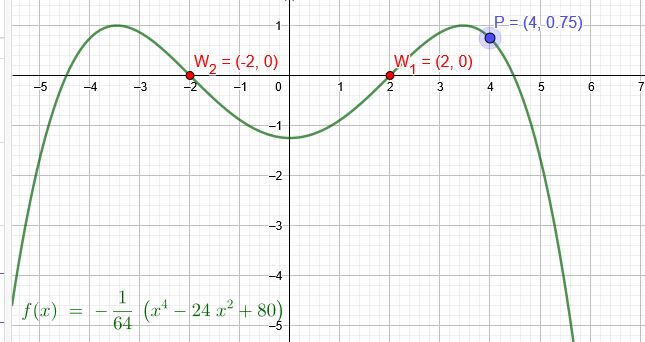
Eine Funktion 4. Grades verläuft symmetrisch zur y-Achse. Der Wendepunkt ist W \((2|0)\).
Sie geht durch den Punkt P \(( 4| 0,75)\).

 \(W_1(2|0)\) →  \(W_2(-2|0)\)

\(f(x)=a(x-2)(x+2)(x-N)(x+N)=a(x^2-4)(x^2-N^2)\\=a(x^4-N^2x^2-4x^2+4N^2)\)

Wendepunkteigenschaft W \((2|...)\)
\(f'(x)=a(4x^3-2N^2x-8x)\)

\(f''(x)=a(12x^2-2N^2-8)\)

\(f''(2)=a(48-2N^2-8)=a(40-2N^2)=0\)

\(N^2=20\):

\(f(x)=a(x^4-24x^2+80)\)

\(( 4| 0,75)\):

\(f(4)=a(256-384+80)=-48a=\frac{3}{4}\)

\(a=-\frac{1}{64}\):

\(f(x)=-\frac{1}{64}(x^4-24x^2+80)\)