Wie untersuche ich dieses uneigentliche Integral auf Konvergenz?

Question

Aufgabe: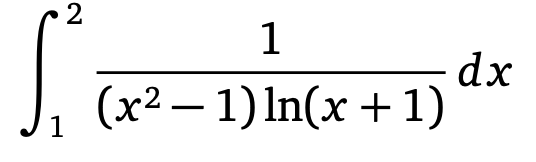

Text erkannt:

\( \int \limits_{1}^{2} \frac{1}{\left(x^{2}-1\right) \ln (x+1)} d x \)

Problem/Ansatz:

Wie untersuche ich dieses uneigentliche Integral auf Konvergenz? Weil im angegebenen Intervall (also untere ist ja 1 und obere 2). Welches Integrationsverfahren benutze ich hier?

Comments

Hallo,

Du hast eine sehr ähnliche Frage gestellt und die Hinweise darauf mit "BesteAntwort" und "vielen, vielen Dank" quittiert. Was ist denn dann noch Deine Frage??

Gruß mathePeter

Answer 1

Hallo

du integrierst gar nicht, da du nur Konvergenz oder nicht untersuchen willst. Nur der Faktor (x-1) im Nenner ist kritisch bei 1 also versuch eine Majorante oder Minorante für  den Integranden in der Nähe von 1 zu finden.

Gruß lul