Hallo,
ich brauche Hilfe bei der Grenzwertberechnung von Folgen.
Konkret:
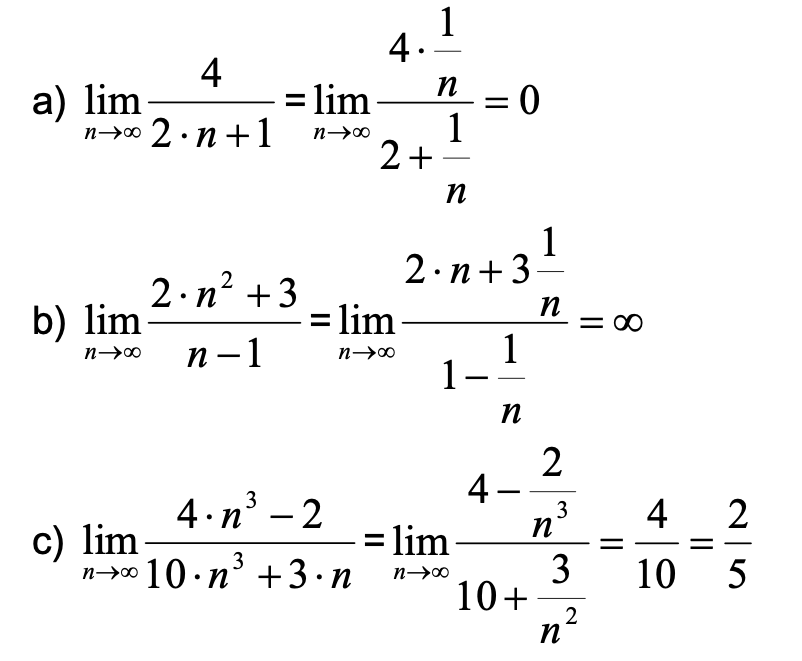
Text erkannt:
a) \( \lim \limits_{n \rightarrow \infty} \frac{4}{2 \cdot n+1}=\lim \limits_{n \rightarrow \infty} \frac{4 \cdot \frac{1}{n}}{2+\frac{1}{n}}=0 \)
b) \( \lim \limits_{n \rightarrow \infty} \frac{2 \cdot n^{2}+3}{n-1}=\lim \limits_{n \rightarrow \infty} \frac{2 \cdot n+3 \frac{1}{n}}{1-\frac{1}{n}}=\infty \)
c) \( \lim \limits_{n \rightarrow \infty} \frac{4 \cdot n^{3}-2}{10 \cdot n^{3}+3 \cdot n}=\lim \limits_{n \rightarrow \infty} \frac{4-\frac{2}{n^{3}}}{10+\frac{3}{n^{2}}}=\frac{4}{10}=\frac{2}{5} \)
Bin bei den Aufgaben leider überfragt, bzw. verstehe die Lösungswege nicht.
Und:
Inwiefern benötige ich das "n gegen unendlich"?
Und was sage ich mit dem Grenzwert nun eigentlich aus; eine Folge strebt gegen einen bestimmten Wert und wird ihn nie erreichen? Wie hängt das mit der Differentialrechnung und dem Ableiten zusammen?
